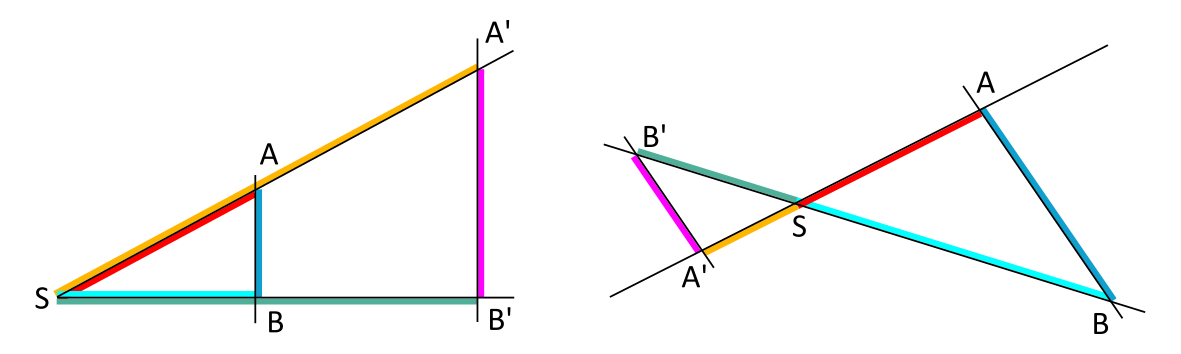Skip to main content Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Triangle Similarity Theorems

The two similarity theorems help us express relationships between lengths of two or more rays that intersect at a point and are all intersected by two parallel lines.

Classic examples include triangular distributed loads in technical mechanics, which need to be cut in arbitrary sections for determining shear forces, or conical or pyramidal bodies, whose diameters often need to be determined as a function of the coordinate \(x\) in strength of materials.

First Similarity Theorem

If two rays with a common vertex \(S\) are intersected by parallel lines that do not pass through the vertex \(S\), then the corresponding segments on one ray are proportional to the corresponding segments on the other ray.

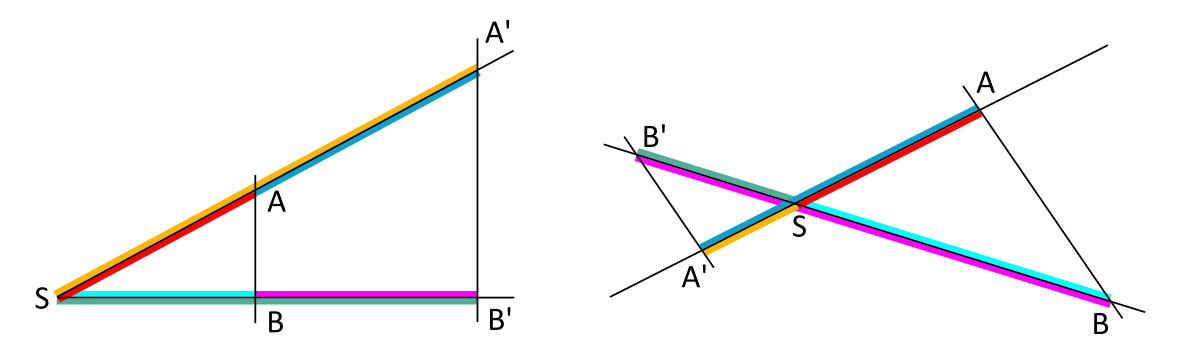
This Figure 1 graphically shows the segments that are proportional according to the first theorem of similar triangles.
Fig. 1: First similarity theorem
$$ \definecolor{lsgreen}{RGB}{79,175,152} \definecolor{lsblue}{RGB}{16,160,205} \definecolor{lsyellow}{RGB}{255,182,0} \begin{aligned} \dfrac{\color{red}\overline{SA}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{lsgreen}\overline{SB~'}}\quad \mathrm{bzw.} \quad \dfrac{\color{red}\overline{SA}}{\color{lsblue}\overline{AA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{fuchsia}\overline{BB~'}}\quad \mathrm{bzw.} \quad \dfrac{\color{lsblue}\overline{AA~'}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{fuchsia}\overline{BB~'}}{\color{lsgreen}\overline{SB~'}} \end{aligned} $$

Second Similarity Theorem

If two rays with a common vertex \(S\) are intersected by parallel lines that do not pass through the vertex \(S\), then the segments on the parallel lines are proportional to the corresponding segments on the rays.

This Figure 2 graphically shows the segments that are in proportion according to the 2nd similarity theorem.
Fig. 2: Second similarity theorem
$$ \definecolor{lsgreen}{RGB}{79,175,152} \definecolor{lsblue}{RGB}{16,160,205} \definecolor{lsyellow}{RGB}{255,182,0} \begin{aligned} \dfrac{\color{lsblue}\overline{AB}}{\color{fuchsia}\overline{A~'B~'}}=\dfrac{\color{red}\overline{SA}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{lsgreen}\overline{SB~'}} \end{aligned} $$
On this page