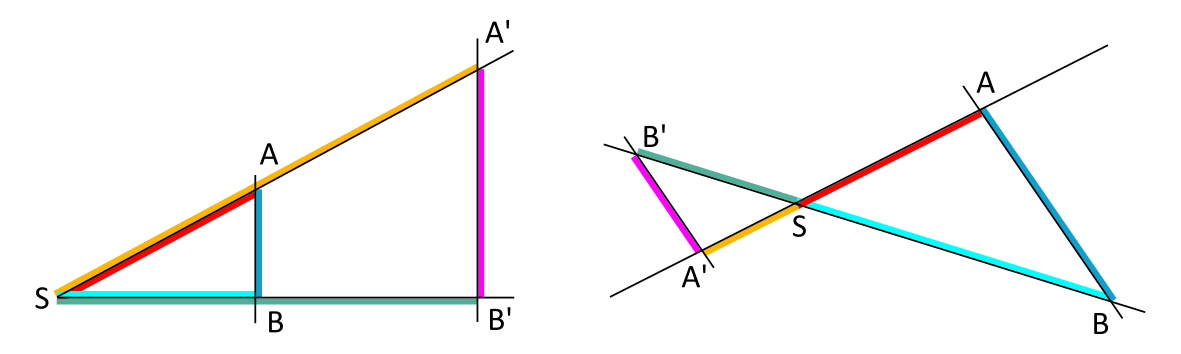1. Strahlensatz
Werden zwei Strahlen, die einen gemeinsamen Scheitelpunkt \(S\) haben, von Parallelen geschnitten, die nicht durch den Scheitelpunkt \(S\) gehen, so sind die Abschnitte auf dem einen Strahl verhältnisgleich mit den zugehörigen Abschnitten auf dem anderen Strahl.
$$
\definecolor{lsgreen}{RGB}{79,175,152}
\definecolor{lsblue}{RGB}{16,160,205}
\definecolor{lsyellow}{RGB}{255,182,0}
\begin{aligned}
\dfrac{\color{red}\overline{SA}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{lsgreen}\overline{SB~'}}\quad \mathrm{bzw.} \quad
\dfrac{\color{red}\overline{SA}}{\color{lsblue}\overline{AA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{fuchsia}\overline{BB~'}}\quad \mathrm{bzw.} \quad
\dfrac{\color{lsblue}\overline{AA~'}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{fuchsia}\overline{BB~'}}{\color{lsgreen}\overline{SB~'}}
\end{aligned} $$
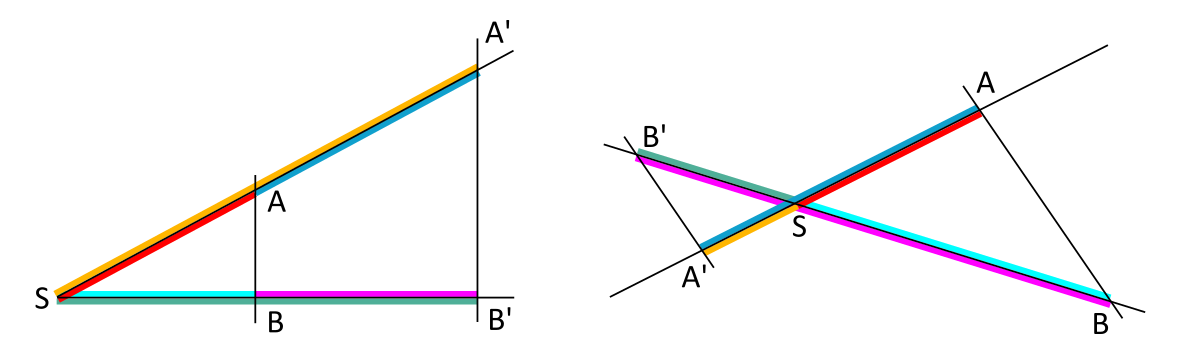
2. Strahlensatz
Werden zwei Strahlen, die einen gemeinsamen Scheitelpunkt \(S\) haben, von Parallelen geschnitten, die nicht durch den Scheitelpunkt \(S\) gehen, so sind die Abschnitte auf den Parallelen verhältnisgleich mit den zugehörigen Abschnitten auf den Strahlen.
$$
\definecolor{lsgreen}{RGB}{79,175,152}
\definecolor{lsblue}{RGB}{16,160,205}
\definecolor{lsyellow}{RGB}{255,182,0}
\begin{aligned}
\dfrac{\color{lsblue}\overline{AB}}{\color{fuchsia}\overline{A~'B~'}}=\dfrac{\color{red}\overline{SA}}{\color{lsyellow}\overline{SA~'}}=\dfrac{\color{aqua}\overline{SB}}{\color{lsgreen}\overline{SB~'}}
\end{aligned} $$