Angle Measures
The angle measure describes the size of an angle and can be expressed in different units, such as degrees (degree measure) or radians (radian measure).
The radian measure \(\theta\) describes the angle \(\varphi\) in terms of the length of the arc on the unit circle that is opposite to the angle \(\varphi\). A complete revolution in radian measure corresponds to the circumference of the unit circle, which is \(2\pi\).
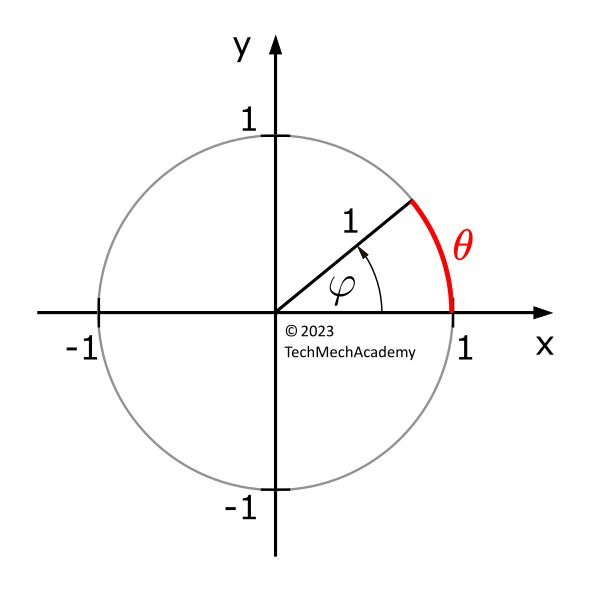
In degree measure, 360° corresponds to a full revolution.
Conversion of Angle Measurements
$$ \begin{alignat}{3}
\text{Radian to degree conversion:}\quad &\varphi &&= \dfrac{180°}{\pi} \cdot \theta\\[12pt]
\text{Degree to radian conversion:}\quad &\theta &&= \dfrac{\pi}{180°} \cdot \varphi
\end{alignat} $$
Definition of the Trigonometric Functions
Trigonometric Functions on the Unit Circle
The trigonometric functions sine, cosine, tangent, and cotangent can be defined on a circle with a radius of 1 (unit circle). For any angle \(\varphi\), formed by a ray passing through the center of the circle and the positive \(x\)-axis, the following relationships hold:
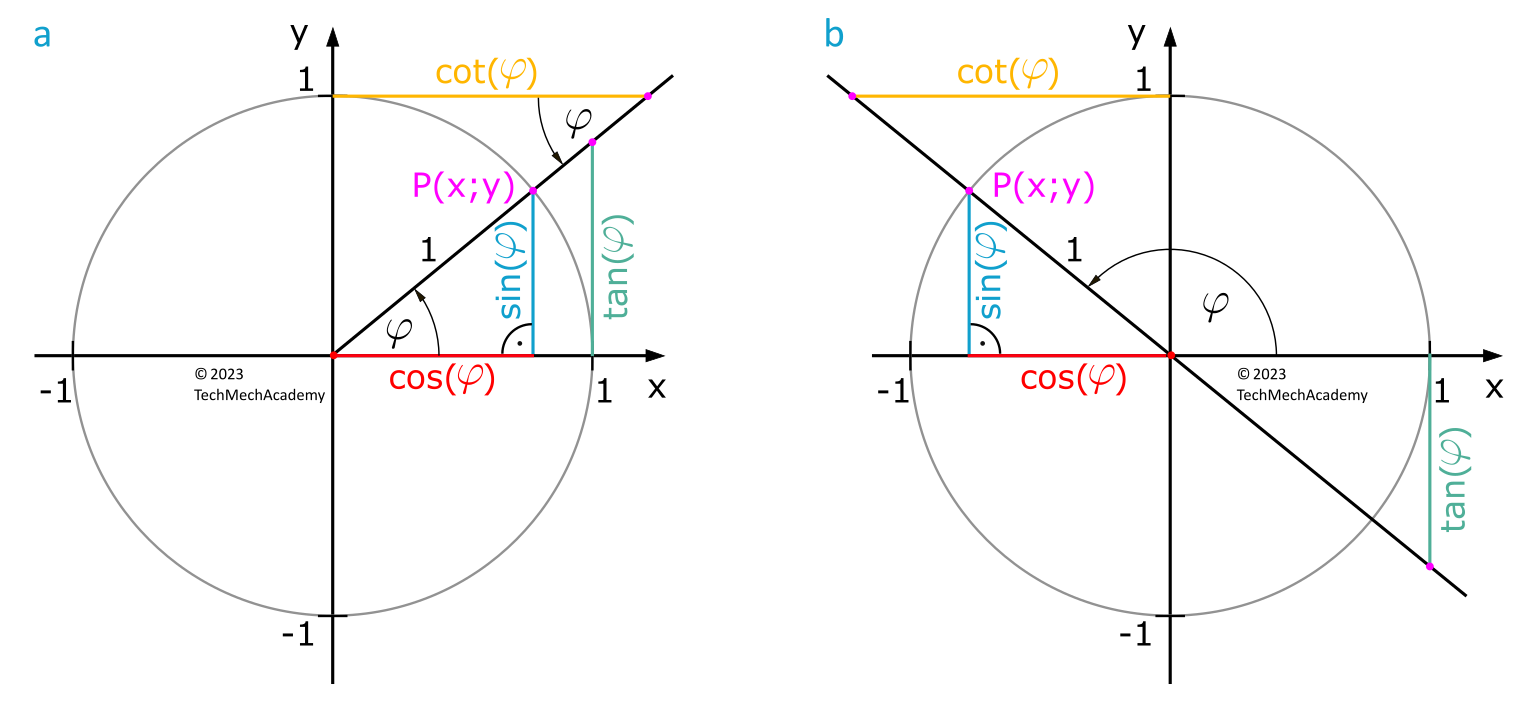
- The sine of an angle \(\varphi\) is the \(y\)-coordinate of the unit circle point \(P\) associated with \(\varphi\).
- The cosine of an angle \(\varphi\) is the \(x\)-coordinate of the unit circle point \(P\) associated with \(\varphi\).
- The tangent of an angle \(\varphi\) is the \(y\)-coordinate of the intersection point of the ray associated with \(\varphi\) and the unit circle tangent through the point \(P(1;0)\).
- The cotangent of an angle \(\varphi\) is the \(x\)-coordinate of the intersection point of the ray associated with \(\varphi\) and the unit circle tangent through the point \(P(0;1)\).
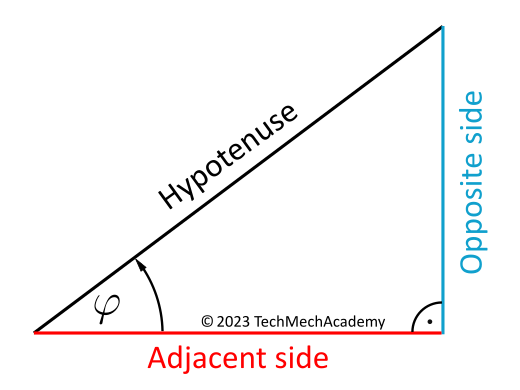
Trigonometric functions in a right-angled Triangle
The definitions derived from the unit circle in Figure 2a can be applied to a right-angled triangle. They hold for both angles that are different from 90°. In this case, the hypotenuse is always the longest side of the right-angled triangle and is opposite to the right angle. The adjacent side forms the angle with the hypotenuse, and the opposite side is positioned opposite to the angle.
$$ \begin{aligned}
\sin(\varphi) &= \dfrac{\mathrm{Opposite~ side}}{\mathrm{Hypotenuse}}\\[7pt]
\cos(\varphi) &= \dfrac{\mathrm{Adjacent~ side}}{\mathrm{Hypotenuse}}\\[7pt]
\tan(\varphi) &= \dfrac{\mathrm{Opposite~ side}}{\mathrm{Adjacent~ side}}\\[7pt]
\cot(\varphi) &= \dfrac{\mathrm{Adjacent~ side}}{\mathrm{Opposite~ side}}
\end{aligned} $$
Quadrant Rule
The quadrant rule (also known as the sign rule) describes in which quadrant of a coordinate system the value of a trigonometric function is positive or negative.
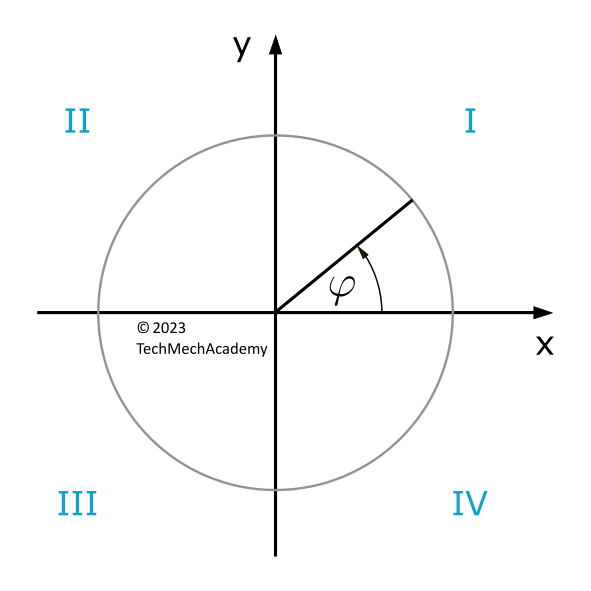
| I | II | III | IV | |
| \(\sin(\varphi)\) | + | + | - | - |
| \(\cos(\varphi)\) | + | - | - | + |
| \(\tan(\varphi)\) | + | - | + | - |
| \(\cot(\varphi)\) | + | - | + | - |
Sine and Cosine Functions
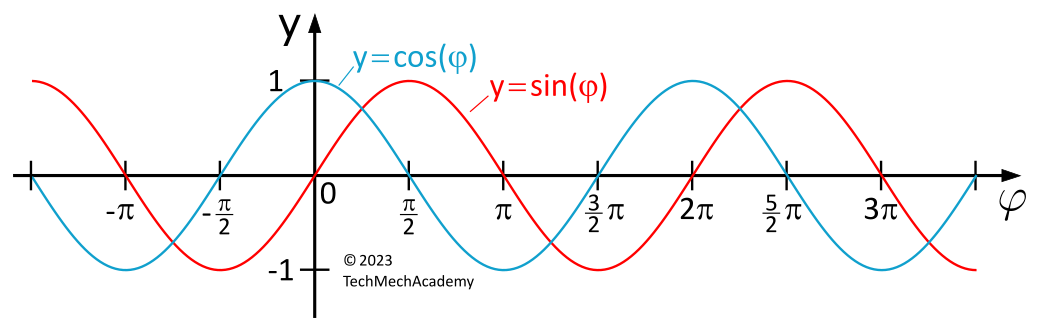
| Properties (\(k \in \mathbb{Z})\) | \(y=\sin(\varphi)\) | \(y=\cos(\varphi)\) |
| Domain | \(-\infty < \varphi < +\infty\) | |
| Range | \(-1 \leq y \leq +1\) | |
| Period (smallest) | \(2\pi\) | |
| Symmetry | ungerade | gerade |
| Zero crossings (or roots) | \(\varphi_k = k \cdot \pi\) | \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Relative maxima | \(\varphi_k = \dfrac{\pi}{2} + k \cdot 2\pi\) | \(\varphi_k = k \cdot 2\pi\) |
| Relative minima | \(\varphi_k = \dfrac{3}{2}\pi + k \cdot 2\pi\) | \(\varphi_k = \pi + k \cdot 2\pi\) |
For all \(\varphi \in \mathbb{R}\), the following properties hold:
$$ \begin{alignat}{3}
\sin\Bigl(\varphi + \dfrac{\pi}{2}\Bigr) &= &&\cos(\varphi) \\[7pt]
\sin\Bigl(\varphi - \dfrac{\pi}{2}\Bigr) &= -&&\cos(\varphi) \\[7pt]
\sin(\pi - \varphi) &= &&\sin(\varphi) \\[7pt]
\sin(\pi + \varphi) &= -&&\sin(\varphi) \\[7pt]
\sin(- \varphi) = \sin(2\pi - \varphi) &= -&&\sin(\varphi)
\end{alignat} $$
$$ \begin{alignat}{3}
\cos\Bigl(\varphi + \dfrac{\pi}{2}\Bigr) &= -&&\sin(\varphi) \\[7pt]
\cos\Bigl(\varphi - \dfrac{\pi}{2}\Bigr) &= &&\sin(\varphi) \\[7pt]
\cos(\pi - \varphi) &= -&&\cos(\varphi) \\[7pt]
\cos(\pi + \varphi) &= -&&\cos(\varphi) \\[7pt]
\cos(- \varphi) = \cos(2\pi - \varphi) &= &&\cos(\varphi)
\end{alignat} $$
The Tangent Function
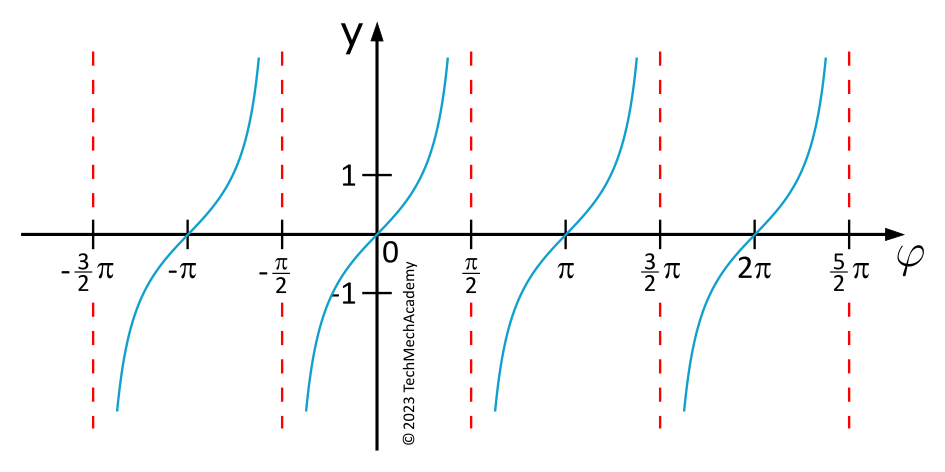
| Properties (\(k \in \mathbb{Z})\) | \(y=\tan(\varphi)\) |
| Domain | \(\varphi \in \mathbb{R}\) mit Ausnahme der Stellen \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Range | \(-\infty < y < +\infty\) |
| Period (smallest) | \(\pi\) |
| Symmetry | ungerade |
| Zero crossings (or roots) | \(\varphi_k = k \cdot \pi\) |
| Poles | \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Vertical asymptotes | \(\varphi = \dfrac{\pi}{2} + k \cdot \pi\) |
The tangent function does not have any extrema.
For all \(\varphi \in \mathbb{R}~ \backslash ~\{\frac{\pi}{2}+k\cdot\pi, ~k\in\mathbb{Z}\}\) the following properties hold for the tangent function:
$$ \begin{aligned}
\tan(\pi + k\varphi) &= \tan(\varphi) \\[7pt]
\tan(- \varphi) &= -\tan(\varphi)
\end{aligned} $$
Important Relationships between the Trigonometric Functions
Relationship between Sine and Cosine Functions
$$ \begin{aligned}
\cos(\varphi) &= \sin\biggl(\varphi+\dfrac{\pi}{2}\biggr) \\[7pt]
\sin(\varphi) &= \cos\biggl(\varphi-\dfrac{\pi}{2}\biggr)
\end{aligned} $$
The cosine function leads the sine function by \(\frac{\pi}{2}\), while the sine function lags behind the cosine function by \(\frac{\pi}{2}\).
Trigonometric Pythagorean Theorem
$$ \begin{aligned}
\sin^2(\varphi) + \cos^2(\varphi) &= 1
\end{aligned} $$
Elementary Relationships between Sine, Cosine, Tangent, and Cotangent Functions
$$ \begin{aligned}
\tan(\varphi) &= \dfrac{\sin(\varphi)}{\cos(\varphi)}=\dfrac{1}{\cot(\varphi)} \\[7pt]
\cot(\varphi) &= \dfrac{\cos(\varphi)}{\sin(\varphi)}=\dfrac{1}{\tan(\varphi)}
\end{aligned} $$
Conversions between Trigonometric Functions
| \(\sin(\varphi)\) | \(\cos(\varphi)\) | \(\tan(\varphi)\) | \(\cot(\varphi)\) | |
| \(\sin(\varphi)\) | — | \(\pm\sqrt{1-\cos^2(\varphi})\) | \(\pm \dfrac{\tan(\varphi)}{\sqrt{1+\tan^2(\varphi})}\) | \(\pm \dfrac{1}{\sqrt{1+\cot^2(\varphi})}\) |
| \(\cos(\varphi)\) | \(\pm\sqrt{1-\sin^2(\varphi})\) | — | \(\pm \dfrac{1}{\sqrt{1+\tan^2(\varphi})}\) | \(\pm \dfrac{\cot(\varphi)}{\sqrt{1+\cot^2(\varphi})}\) |
| \(\tan(\varphi)\) | \(\pm \dfrac{\sin(\varphi)}{\sqrt{1-\sin^2(\varphi)}}\) | \(\pm \dfrac{\sqrt{1-\cos^2(\varphi)}}{\cos(\varphi)}\) | — | \(\dfrac{1}{\cot(\varphi)}\) |
| \(\cot(\varphi)\) | \(\pm \dfrac{\sqrt{1-\sin^2(\varphi)}}{\sin(\varphi)}\) | \(\pm \dfrac{\cos(\varphi)}{\sqrt{1-\cos^2(\varphi)}}\) | \(\dfrac{1}{\tan(\varphi)}\) | — |
The sign is determined according to the quadrant rule.
Formulas for Trigonometric Functions
Addition Theorems for Calculating the Sum and Difference of Angle Values
$$ \begin{aligned}
\sin(\varphi_1\pm\varphi_2) &= \sin(\varphi_1) \cdot \cos(\varphi_2) \pm \cos(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\cos(\varphi_1\pm\varphi_2) &= \cos(\varphi_1) \cdot \cos(\varphi_2) \mp \sin(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\tan(\varphi_1\pm\varphi_2) &= \dfrac{\tan(\varphi_1) \pm \tan(\varphi_2)}{1 \mp \tan(\varphi_1) \cdot \tan(\varphi_2)}\\[7pt]
\cot(\varphi_1\pm\varphi_2) &= \dfrac{\cot(\varphi_1) \cdot \cot(\varphi_2) \mp 1}{\cot(\varphi_2) \pm \cot(\varphi_1)}
\end{aligned} $$
Formulas for Half-Angles
$$ \begin{aligned}
\sin\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 - \cos(\varphi)}{2}}\\[7pt]
\cos\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 + \cos(\varphi)}{2}}\\[7pt]
\tan\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 -\cos(\varphi)}{1 +\cos(\varphi)}} = \dfrac{\sin(\varphi)}{1 + \cos(\varphi)} = \dfrac{1 - \cos(\varphi)}{\sin(\varphi)}\\[7pt]
\cot\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 +\cos(\varphi)}{1 -\cos(\varphi)}} = \dfrac{\sin(\varphi)}{1 - \cos(\varphi)} = \dfrac{1 + \cos(\varphi)}{\sin(\varphi)}\\[7pt]
\end{aligned} $$
The sign is determined according to the quadrant of the argument \(\dfrac{\varphi}{2}\) using the quadrant rule.
Formulas for Double Angles
$$ \begin{aligned}
\sin(2\varphi) &= 2 \cdot \sin(\varphi) \cdot \cos(\varphi) = \dfrac{2 \cdot \tan(\varphi)}{1 + \tan^2(\varphi)}\\[7pt]
\cos(2\varphi) &= \cos^2(\varphi) - \sin^2(\varphi) = 1 - 2 \cdot \sin^2(\varphi) = 2 \cdot \cos^2(\varphi)-1 = \dfrac{1 - \tan^2(\varphi)}{1 + \tan^2(\varphi)}\\[7pt]
\tan(2\varphi) &= \dfrac{2 \cdot \tan(\varphi)}{1 - \tan^2(\varphi)} = \dfrac{2}{\cot(\varphi) - \tan(\varphi)}\\[7pt]
\cot(2\varphi) &= \dfrac{\cot^2(\varphi)-1}{2 \cdot \cot(\varphi)} = \dfrac{\cot(\varphi) - \tan(\varphi)}{2}
\end{aligned} $$
Formulas for Triple Angles
$$ \begin{aligned}
\sin(3\varphi) &= 3 \cdot \sin(\varphi) - 4 \cdot \sin^3(\varphi)\\[7pt]
\cos(3\varphi) &= 4 \cdot \cos^3(\varphi) - 3 \cdot \cos(\varphi)\\[7pt]
\tan(3\varphi) &= \dfrac{3 \cdot \tan(\varphi) - \tan^3(\varphi)}{1 - 3 \cdot \tan^2(\varphi)}\\[7pt]
\cot(3\varphi) &= \dfrac{\cot^3(\varphi) - 3 \cdot \cot(\varphi)}{3 \cdot \cot^2(\varphi)-1}
\end{aligned} $$
Formulas for Powers of Trigonometric Terms
$$ \begin{aligned}
\sin^2(\varphi) &= \dfrac{1}{2} \cdot \bigl[1 - \cos(2\varphi)\bigr]\\[7pt]
\sin^3(\varphi) &= \dfrac{1}{4} \cdot \bigl[3 \cdot \sin(\varphi) - \sin(3\varphi)\bigr]\\[7pt]
\sin^4(\varphi) &= \dfrac{1}{8} \cdot \bigl[\cos(4 \varphi) - 4 \cdot \cos(2 \varphi) + 3\bigr]
\end{aligned} $$
$$ \begin{aligned}
\cos^2(\varphi) &= \dfrac{1}{2} \cdot \bigl[1 + \cos(2\varphi)\bigr]\\[7pt]
\cos^3(\varphi) &= \dfrac{1}{4} \cdot \bigl[3 \cdot \cos(\varphi) + \cos(3\varphi)\bigr]\\[7pt]
\cos^4(\varphi) &= \dfrac{1}{8} \cdot \bigl[\cos(4 \varphi) + 4 \cdot \cos(2 \varphi) + 3\bigr]
\end{aligned} $$
Formulas for Sums and Differences of Trigonometric Terms
$$ \begin{aligned}
\sin(\varphi_1) + \sin(\varphi_2) &= 2 \cdot \sin\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\sin(\varphi_1) - \sin(\varphi_2) &= 2 \cdot \sin\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr)\\[7pt]
\cos(\varphi_1) + \cos(\varphi_2) &= 2 \cdot \cos\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\cos(\varphi_1) - \cos(\varphi_2) &= -2 \cdot \sin\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \sin\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\tan(\varphi_1) + \tan(\varphi_2) &= \dfrac{\sin(\varphi_1+\varphi_2)}{\cos(\varphi_1) \cdot \cos(\varphi_2)}\\[7pt]
\tan(\varphi_1) - \tan(\varphi_2) &= \dfrac{\sin(\varphi_1-\varphi_2)}{\cos(\varphi_1) \cdot \cos(\varphi_2)}\\[7pt]
\cot(\varphi_1) + \cot(\varphi_2) &= \dfrac{\sin(\varphi_1+\varphi_2)}{\sin(\varphi_1) \cdot \sin(\varphi_2)}\\[7pt]
\cot(\varphi_1) - \cot(\varphi_2) &= -\dfrac{\sin(\varphi_1-\varphi_2)}{\sin(\varphi_1) \cdot \sin(\varphi_2)}
\end{aligned} $$
$$ \begin{aligned}
\sin(\varphi_1 + \varphi_2) + \sin(\varphi_1 - \varphi_2) &= 2 \cdot \sin(\varphi_1) \cdot \cos(\varphi_2)\\[7pt]
\sin(\varphi_1 + \varphi_2) - \sin(\varphi_1 - \varphi_2) &= 2 \cdot \cos(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\cos(\varphi_1 + \varphi_2) + \cos(\varphi_1 - \varphi_2) &= 2 \cdot \cos(\varphi_1) \cdot \cos(\varphi_2)\\[7pt]
\cos(\varphi_1 + \varphi_2) - \cos(\varphi_1 - \varphi_2) &= -2 \cdot \sin(\varphi_1) \cdot \sin(\varphi_2)
\end{aligned} $$
Formulas for Products of Trigonometric Terms
$$ \begin{aligned}
\sin(\varphi_1) \cdot \sin(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\cos(\varphi_1-\varphi_2) - \cos(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\cos(\varphi_1) \cdot \cos(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\cos(\varphi_1-\varphi_2) + \cos(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\sin(\varphi_1) \cdot \cos(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\sin(\varphi_1-\varphi_2) + \sin(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\sin(\varphi) \cdot \cos(\varphi) &= \dfrac{1}{2} \cdot \Bigl(\sin(2 \varphi)\Bigr)\\[7pt]
\tan(\varphi_1) \cdot \tan(\varphi_2) &= \dfrac{\tan(\varphi_1) + \tan(\varphi_2)}{\cot(\varphi_1) + \cot(\varphi_2)} = -\dfrac{\tan(\varphi_1) - \tan(\varphi_2)}{\cot(\varphi_1) - \cot(\varphi_2)}\\[7pt]
\cot(\varphi_1) \cdot \cot(\varphi_2) &= \dfrac{\cot(\varphi_1) + \cot(\varphi_2)}{\tan(\varphi_1) + \tan(\varphi_2)} = -\dfrac{\cot(\varphi_1) - \cot(\varphi_2)}{\tan(\varphi_1) - \tan(\varphi_2)}\\[7pt]
\tan(\varphi_1) \cdot \cot(\varphi_2) &= \dfrac{\tan(\varphi_1) + \cot(\varphi_2)}{\cot(\varphi_1) + \tan(\varphi_2)} = -\dfrac{\tan(\varphi_1) - \cot(\varphi_2)}{\cot(\varphi_1) - \tan(\varphi_2)}
\end{aligned} $$
On this Page