Skip to main content Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Rigid Body Statics

Central Force Systems: Forces with a Common Point of Application

In engineering mechanics, the analysis of forces acting on an object plays a central role. An important special case is the central force system, where all these forces have a common point of application. In this chapter, we will explore the properties and analysis of central force systems and explore:

  • Definition and Properties: What is a central force system? What special properties distinguish it?
  • Basic Tasks of Rigid Body Statics for Central Force Systems:
    • Reduction: Reducing a system of multiple forces to a single point (center of force).
    • Equilibrium: Determining whether a body remains at rest or moves under the action of forces.
    • Decomposition: Decomposing a force into several individual forces.

Are you ready to unlock these secrets?

On this Page
Table of Contents

1. Introduction

In engineering mechanics, the study of forces and their effects on bodies plays a central role. An important special case is the central force system, in which several forces act on a common point of application. In this chapter, we will take a closer look at the properties and special features of these systems.

Definition and Properties

A central force system exists when all lines of action of the attacking forces intersect at a point.

This point is called the central point of the system. The number of forces in such a system can be arbitrary, but there must be at least one force present.

Important properties:
  • Translational motion: The resultant force of a central force system always causes a translational motion of the body, i.e. a straight-line motion without rotation.
  • Moment-free: Since the lines of action of all forces pass through the center of gravity, the total torque of the system is equal to zero.
  • Simplification of the analysis: The analysis of a central force system is much simpler than that of a general force system, since only the resultant force and the center of gravity are relevant.
Example

Imagine you have a lamp hanging from two ropes. What happens then? What forces are acting? And how can we calculate that?

This figure 3.1.1 shows a room lamp hanging from the ceiling with two ropes.
Fig. 3.1.1: Beam with Lamp

First, we mentally cut the lamp from the beam at the ropes. This is how we see the reaction forces F1 and F2 in the ropes. The lines of action of these forces run along the ropes and intersect at a point P.

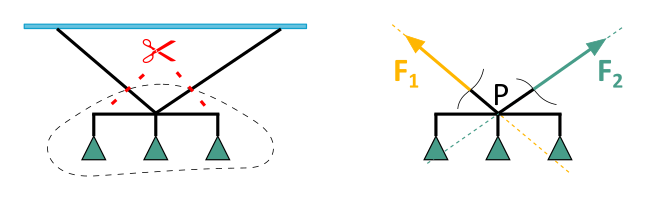
This figure 3.1.2 shows the cross-section of the room lamp.
Fig. 3.1.2: Cross-section of Lamp

The weight force of the lamp G also acts through this point P. So we have a central force system: All lines of action of the forces intersect at a point.

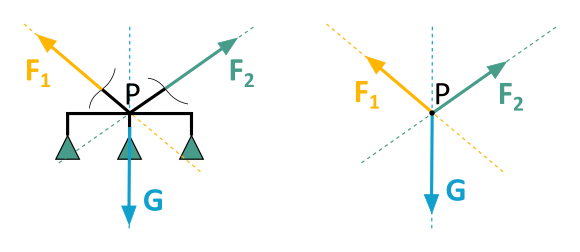
This figure 3.1.3 shows the central force system on the lamp.
Fig. 3.1.3: Lamp as Central Force System

Is everything clear so far? Here is a short quiz question for self-assessment:

Why are the two forces F1 and F2 each assumed to be at an angle upwards?

Both must of course be tensile forces, since ropes can only absorb tensile forces in the direction of their longitudinal axis.

The Three Basic Tasks of Engineering Mechanics

With central force systems, we can do three important things:

  1. Reduction to a single force:

    We can combine all individual forces into a single force, the so-called resultant. This is practical, for example, if we want to calculate the total load on a component.

  2. Conditions for equilibrium:

    A body is in equilibrium if the sum of all forces and moments is equal to zero. For central force systems, this means: The resultant must be equal to zero.

  3. Decomposition of a force:

    We can decompose a force into two or more other forces. This is useful, for example, if we want to calculate the forces in the individual ropes of the lamp.

Graphical and Numerical Analysis

Central force systems can be investigated both graphically and numerically.

  1. Graphically:

    With the help of position and force diagrams, we can represent the forces graphically and determine their effects on the body.

  2. Numerically:

    With the help of vector calculus, we can solve the equations of statics and calculate the required quantities.

Summary

Central force systems are an important topic in statics. With the three basic tasks - reduction to a single force, conditions for equilibrium and decomposition of a force - we can solve many static problems.

By the way: The central force system is a special case. Later we will get to know the general force system. That will be a bit more exciting.

So, enough theory! Let's get to work on the tasks!