Winkelmaße
Das Winkelmaß beschreibt die Größe eines Winkels und kann in verschiedenen Einheiten angegeben werden, wie beispielsweise Grad (Gradmaß) oder Radiant (Bogenmaß).
Das Bogenmaß \(\theta\) beschreibt den Winkel \(\varphi\) mit der Länge des Bogens auf dem Einheitskreis, der dem Winkel \(\varphi\) gegenüberliegt. Eine volle Umdrehung entspricht im Bogenmaß demnach dem Umfang des Einheitskreises, also \(2\pi\).
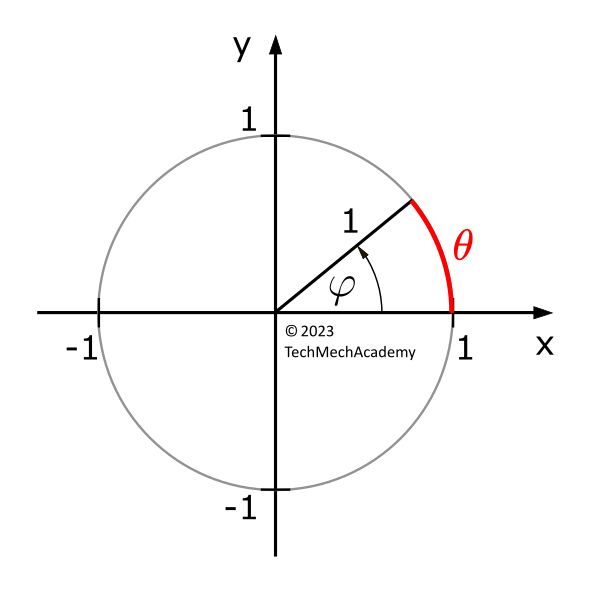
Im Gradmaß entsprechen 360° einer vollen Umdrehung.
Definition der Winkelfunktionen
Winkelfunktionen am Einheitskreis
Die trigonometrischen Funktionen Sinus, Kosinus, Tangens und Kotangens können an einem Kreis mit Radius 1 (Einheitskreis) definiert werden. Für einen beliebigen Winkel \(\varphi\), den ein durch den Kreismittelpunkt verlaufender Strahl mit der positiven \(x\)-Achse bildet, gilt:
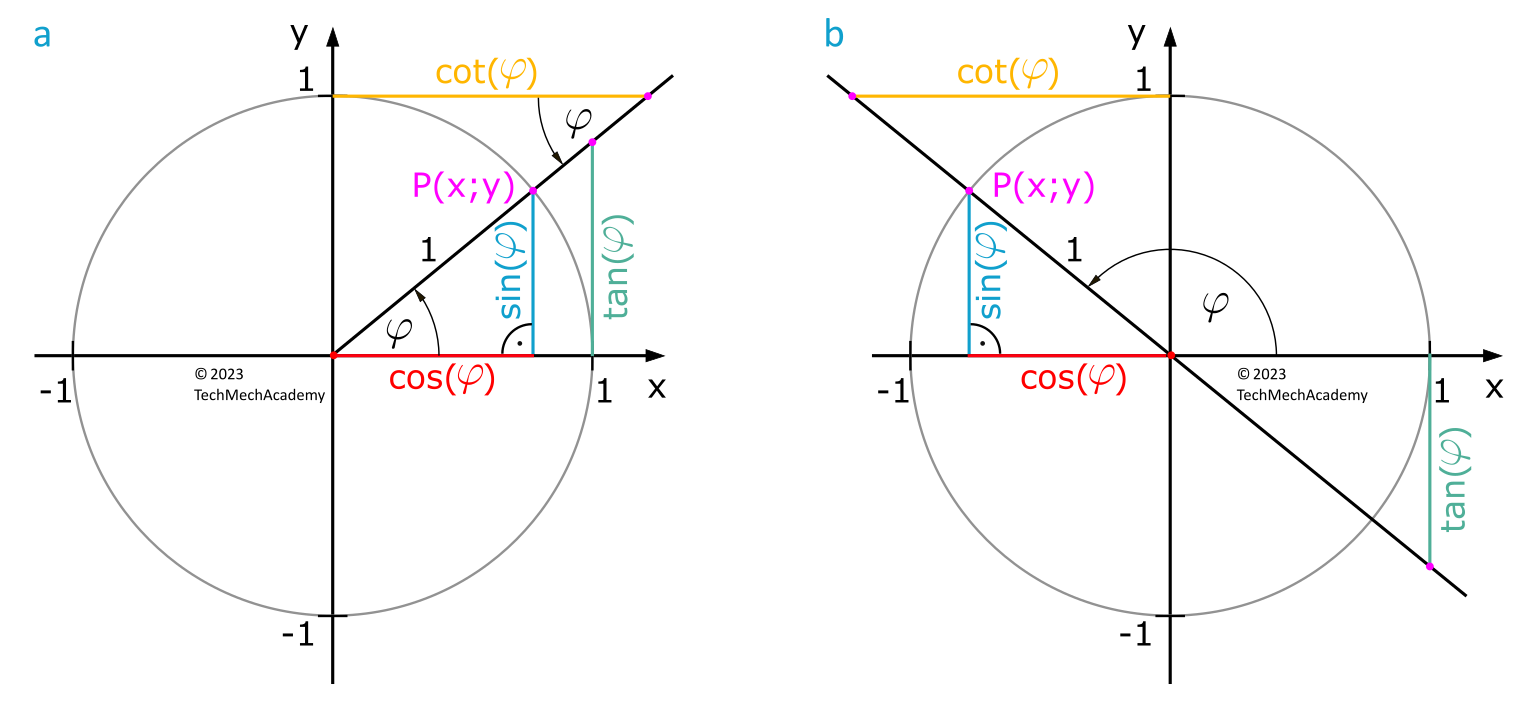
- Der Sinus eines Winkels \(\varphi\) ist die \(y\)-Koordinate des zu \(\varphi\) gehörenden Einheitskreispunktes \(P\).
- Der Kosinus eines Winkels \(\varphi\) ist die \(x\)-Koordinate des zu \(\varphi\) gehörenden Einheitskreispunktes \(P\).
- Der Tangens eines Winkels \(\varphi\) ist die \(y\)-Koordinate des Schnittpunktes des zu \(\varphi\) gehörenden Strahles mit der Einheitskreistangente durch den Punkt \(P(1;0)\).
- Der Kotangens eines Winkels \(\varphi\) ist die \(x\)-Koordinate des Schnittpunktes des zu \(\varphi\) gehörenden Strahles mit der Einheitskreistangente durch den Punkt \(P(0;1)\).
Winkelfunktionen im rechtwinkligen Dreieck
Die im Einheitskreis nach Abbildung 2a hergeleiteten Definitionen können auf ein rechtwinkliges Dreieck übertragen werden. Sie gelten für beide der von 90° verschiedenen Winkel. Dabei ist die Hypotenuse stets die dem rechten Winkel gegenüber liegende längste Seite des rechtwinkligen Dreiecks, die Ankathete bildet mit der Hypotenuse den Winkel und die Gegenkathete liegt dem Winkel gegenüber.
$$ \begin{aligned}
\sin(\varphi) &= \dfrac{\mathrm{Gegenkathete}}{\mathrm{Hypotenuse}}\\[7pt]
\cos(\varphi) &= \dfrac{\mathrm{Ankathete}}{\mathrm{Hypotenuse}}\\[7pt]
\tan(\varphi) &= \dfrac{\mathrm{Gegenkathete}}{\mathrm{Ankathete}}\\[7pt]
\cot(\varphi) &= \dfrac{\mathrm{Ankathete}}{\mathrm{Gegenkathete}}
\end{aligned} $$
Quadrantenregel
Die Quadrantenregel (auch: Vorzeichenregel) beschreibt, in welchem Quadranten eines Koordinatensystems ein Funktionswert einer trigonometrischen Funktion positiv oder negativ ist.
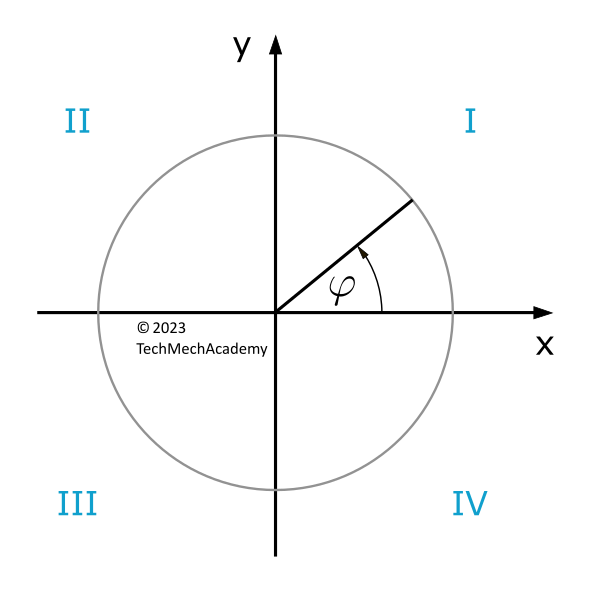
| I | II | III | IV | |
| \(\sin(\varphi)\) | + | + | - | - |
| \(\cos(\varphi)\) | + | - | - | + |
| \(\tan(\varphi)\) | + | - | + | - |
| \(\cot(\varphi)\) | + | - | + | - |
Sinus- und Kosinusfunktion
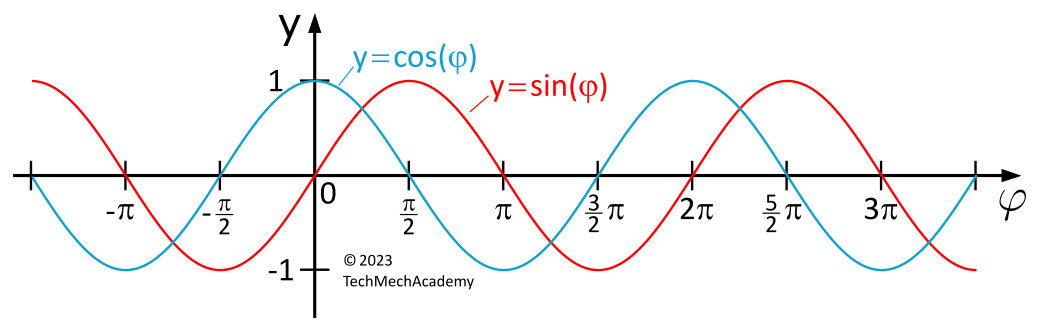
| Eigenschaften (\(k \in \mathbb{Z})\) | \(y=\sin(\varphi)\) | \(y=\cos(\varphi)\) |
| Definitionsbereich | \(-\infty < \varphi < +\infty\) | |
| Wertebereich | \(-1 \leq y \leq +1\) | |
| Periode (kleinste) | \(2\pi\) | |
| Symmetrie | ungerade | gerade |
| Nullstellen | \(\varphi_k = k \cdot \pi\) | \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Relative Maxima | \(\varphi_k = \dfrac{\pi}{2} + k \cdot 2\pi\) | \(\varphi_k = k \cdot 2\pi\) |
| Relative Minima | \(\varphi_k = \dfrac{3}{2}\pi + k \cdot 2\pi\) | \(\varphi_k = \pi + k \cdot 2\pi\) |
Für alle \(\varphi \in \mathbb{R}\) gilt:
$$ \begin{alignat}{3}
\sin\Bigl(\varphi + \dfrac{\pi}{2}\Bigr) &= &&\cos(\varphi) \\[7pt]
\sin\Bigl(\varphi - \dfrac{\pi}{2}\Bigr) &= -&&\cos(\varphi) \\[7pt]
\sin(\pi - \varphi) &= &&\sin(\varphi) \\[7pt]
\sin(\pi + \varphi) &= -&&\sin(\varphi) \\[7pt]
\sin(- \varphi) = \sin(2\pi - \varphi) &= -&&\sin(\varphi)
\end{alignat} $$
$$ \begin{alignat}{3}
\cos\Bigl(\varphi + \dfrac{\pi}{2}\Bigr) &= -&&\sin(\varphi) \\[7pt]
\cos\Bigl(\varphi - \dfrac{\pi}{2}\Bigr) &= &&\sin(\varphi) \\[7pt]
\cos(\pi - \varphi) &= -&&\cos(\varphi) \\[7pt]
\cos(\pi + \varphi) &= -&&\cos(\varphi) \\[7pt]
\cos(- \varphi) = \cos(2\pi - \varphi) &= &&\cos(\varphi)
\end{alignat} $$
Tangensfunktion
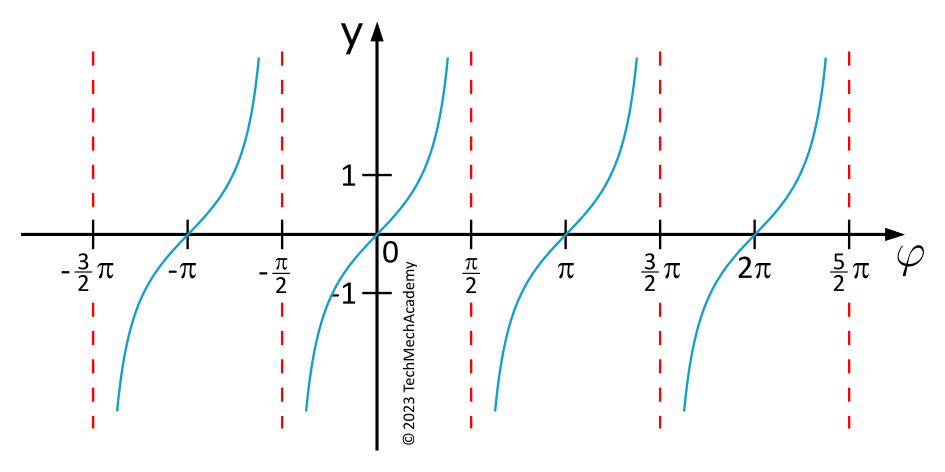
| Eigenschaften (\(k \in \mathbb{Z})\) | \(y=\tan(\varphi)\) |
| Definitionsbereich | \(\varphi \in \mathbb{R}\) mit Ausnahme der Stellen \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Wertebereich | \(-\infty < y < +\infty\) |
| Periode (kleinste) | \(\pi\) |
| Symmetrie | ungerade |
| Nullstellen | \(\varphi_k = k \cdot \pi\) |
| Pole | \(\varphi_k = \dfrac{\pi}{2} + k \cdot \pi\) |
| Senkrechte Asymptoten | \(\varphi = \dfrac{\pi}{2} + k \cdot \pi\) |
Der Tangens hat keine Extrema.
Für alle \(\varphi \in \mathbb{R}~ \backslash ~\{\frac{\pi}{2}+k\cdot\pi, ~k\in\mathbb{Z}\}\) gilt:
$$ \begin{aligned}
\tan(\pi + k\varphi) &= \tan(\varphi) \\[7pt]
\tan(- \varphi) &= -\tan(\varphi)
\end{aligned} $$
Wichtige Beziehungen zwischen den Winkelfunktionen
Beziehung zwischen Sinus- und Kosinus-Funktion
$$ \begin{aligned}
\cos(\varphi) &= \sin\biggl(\varphi+\dfrac{\pi}{2}\biggr) \\[7pt]
\sin(\varphi) &= \cos\biggl(\varphi-\dfrac{\pi}{2}\biggr)
\end{aligned} $$
Der Kosinus läuft dem Sinus um \(\frac{\pi}{2}\) voraus, der Sinus läuft dem Kosinus um \(\frac{\pi}{2}\) hinterher.
Trigonometrischer Pythagoras
$$ \begin{aligned}
\sin^2(\varphi) + \cos^2(\varphi) &= 1
\end{aligned} $$
Elementare Zusammenhänge zwischen Sinus-, Kosinus, Tangens- und Kotangens-Funktion
$$ \begin{aligned}
\tan(\varphi) &= \dfrac{\sin(\varphi)}{\cos(\varphi)}=\dfrac{1}{\cot(\varphi)} \\[7pt]
\cot(\varphi) &= \dfrac{\cos(\varphi)}{\sin(\varphi)}=\dfrac{1}{\tan(\varphi)}
\end{aligned} $$
Umrechnungen zwischen den Winkelfunktionen
| \(\sin(\varphi)\) | \(\cos(\varphi)\) | \(\tan(\varphi)\) | \(\cot(\varphi)\) | |
| \(\sin(\varphi)\) | — | \(\pm\sqrt{1-\cos^2(\varphi})\) | \(\pm \dfrac{\tan(\varphi)}{\sqrt{1+\tan^2(\varphi})}\) | \(\pm \dfrac{1}{\sqrt{1+\cot^2(\varphi})}\) |
| \(\cos(\varphi)\) | \(\pm\sqrt{1-\sin^2(\varphi})\) | — | \(\pm \dfrac{1}{\sqrt{1+\tan^2(\varphi})}\) | \(\pm \dfrac{\cot(\varphi)}{\sqrt{1+\cot^2(\varphi})}\) |
| \(\tan(\varphi)\) | \(\pm \dfrac{\sin(\varphi)}{\sqrt{1-\sin^2(\varphi)}}\) | \(\pm \dfrac{\sqrt{1-\cos^2(\varphi)}}{\cos(\varphi)}\) | — | \(\dfrac{1}{\cot(\varphi)}\) |
| \(\cot(\varphi)\) | \(\pm \dfrac{\sqrt{1-\sin^2(\varphi)}}{\sin(\varphi)}\) | \(\pm \dfrac{\cos(\varphi)}{\sqrt{1-\cos^2(\varphi)}}\) | \(\dfrac{1}{\tan(\varphi)}\) | — |
Das Vorzeichen wird nach der Quadrantenregel bestimmt.
Formeln für Winkelfunktionen
Additionstheoreme für die Berechnung von Summe und Differenz von Winkelwerten
$$ \begin{aligned}
\sin(\varphi_1\pm\varphi_2) &= \sin(\varphi_1) \cdot \cos(\varphi_2) \pm \cos(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\cos(\varphi_1\pm\varphi_2) &= \cos(\varphi_1) \cdot \cos(\varphi_2) \mp \sin(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\tan(\varphi_1\pm\varphi_2) &= \dfrac{\tan(\varphi_1) \pm \tan(\varphi_2)}{1 \mp \tan(\varphi_1) \cdot \tan(\varphi_2)}\\[7pt]
\cot(\varphi_1\pm\varphi_2) &= \dfrac{\cot(\varphi_1) \cdot \cot(\varphi_2) \mp 1}{\cot(\varphi_2) \pm \cot(\varphi_1)}
\end{aligned} $$
Formeln für halbe Winkel
$$ \begin{aligned}
\sin\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 - \cos(\varphi)}{2}}\\[7pt]
\cos\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 + \cos(\varphi)}{2}}\\[7pt]
\tan\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 -\cos(\varphi)}{1 +\cos(\varphi)}} = \dfrac{\sin(\varphi)}{1 + \cos(\varphi)} = \dfrac{1 - \cos(\varphi)}{\sin(\varphi)}\\[7pt]
\cot\Bigl(\dfrac{\varphi}{2}\Bigr) &= \pm \sqrt{\dfrac{1 +\cos(\varphi)}{1 -\cos(\varphi)}} = \dfrac{\sin(\varphi)}{1 - \cos(\varphi)} = \dfrac{1 + \cos(\varphi)}{\sin(\varphi)}\\[7pt]
\end{aligned} $$
Das Vorzeichen ist entsprechend der Größe des Argumentes \(\dfrac{\varphi}{2}\) nach der Quadrantenregel zu bestimmen.
Formeln für doppelte Winkel
$$ \begin{aligned}
\sin(2\varphi) &= 2 \cdot \sin(\varphi) \cdot \cos(\varphi) = \dfrac{2 \cdot \tan(\varphi)}{1 + \tan^2(\varphi)}\\[7pt]
\cos(2\varphi) &= \cos^2(\varphi) - \sin^2(\varphi) = 1 - 2 \cdot \sin^2(\varphi) = 2 \cdot \cos^2(\varphi)-1 = \dfrac{1 - \tan^2(\varphi)}{1 + \tan^2(\varphi)}\\[7pt]
\tan(2\varphi) &= \dfrac{2 \cdot \tan(\varphi)}{1 - \tan^2(\varphi)} = \dfrac{2}{\cot(\varphi) - \tan(\varphi)}\\[7pt]
\cot(2\varphi) &= \dfrac{\cot^2(\varphi)-1}{2 \cdot \cot(\varphi)} = \dfrac{\cot(\varphi) - \tan(\varphi)}{2}
\end{aligned} $$
Formeln für dreifache Winkel
$$ \begin{aligned}
\sin(3\varphi) &= 3 \cdot \sin(\varphi) - 4 \cdot \sin^3(\varphi)\\[7pt]
\cos(3\varphi) &= 4 \cdot \cos^3(\varphi) - 3 \cdot \cos(\varphi)\\[7pt]
\tan(3\varphi) &= \dfrac{3 \cdot \tan(\varphi) - \tan^3(\varphi)}{1 - 3 \cdot \tan^2(\varphi)}\\[7pt]
\cot(3\varphi) &= \dfrac{\cot^3(\varphi) - 3 \cdot \cot(\varphi)}{3 \cdot \cot^2(\varphi)-1}
\end{aligned} $$
Formeln für Potenzen von trigonometrischen Termen
$$ \begin{aligned}
\sin^2(\varphi) &= \dfrac{1}{2} \cdot \bigl[1 - \cos(2\varphi)\bigr]\\[7pt]
\sin^3(\varphi) &= \dfrac{1}{4} \cdot \bigl[3 \cdot \sin(\varphi) - \sin(3\varphi)\bigr]\\[7pt]
\sin^4(\varphi) &= \dfrac{1}{8} \cdot \bigl[\cos(4 \varphi) - 4 \cdot \cos(2 \varphi) + 3\bigr]
\end{aligned} $$
$$ \begin{aligned}
\cos^2(\varphi) &= \dfrac{1}{2} \cdot \bigl[1 + \cos(2\varphi)\bigr]\\[7pt]
\cos^3(\varphi) &= \dfrac{1}{4} \cdot \bigl[3 \cdot \cos(\varphi) + \cos(3\varphi)\bigr]\\[7pt]
\cos^4(\varphi) &= \dfrac{1}{8} \cdot \bigl[\cos(4 \varphi) + 4 \cdot \cos(2 \varphi) + 3\bigr]
\end{aligned} $$
Formeln für Summen und Differenzen von trigonometrischen Termen
$$ \begin{aligned}
\sin(\varphi_1) + \sin(\varphi_2) &= 2 \cdot \sin\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\sin(\varphi_1) - \sin(\varphi_2) &= 2 \cdot \sin\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr)\\[7pt]
\cos(\varphi_1) + \cos(\varphi_2) &= 2 \cdot \cos\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \cos\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\cos(\varphi_1) - \cos(\varphi_2) &= -2 \cdot \sin\Bigl(\dfrac{\varphi_1+\varphi_2}{2}\Bigr) \cdot \sin\Bigl(\dfrac{\varphi_1-\varphi_2}{2}\Bigr)\\[7pt]
\tan(\varphi_1) + \tan(\varphi_2) &= \dfrac{\sin(\varphi_1+\varphi_2)}{\cos(\varphi_1) \cdot \cos(\varphi_2)}\\[7pt]
\tan(\varphi_1) - \tan(\varphi_2) &= \dfrac{\sin(\varphi_1-\varphi_2)}{\cos(\varphi_1) \cdot \cos(\varphi_2)}\\[7pt]
\cot(\varphi_1) + \cot(\varphi_2) &= \dfrac{\sin(\varphi_1+\varphi_2)}{\sin(\varphi_1) \cdot \sin(\varphi_2)}\\[7pt]
\cot(\varphi_1) - \cot(\varphi_2) &= -\dfrac{\sin(\varphi_1-\varphi_2)}{\sin(\varphi_1) \cdot \sin(\varphi_2)}
\end{aligned} $$
$$ \begin{aligned}
\sin(\varphi_1 + \varphi_2) + \sin(\varphi_1 - \varphi_2) &= 2 \cdot \sin(\varphi_1) \cdot \cos(\varphi_2)\\[7pt]
\sin(\varphi_1 + \varphi_2) - \sin(\varphi_1 - \varphi_2) &= 2 \cdot \cos(\varphi_1) \cdot \sin(\varphi_2)\\[7pt]
\cos(\varphi_1 + \varphi_2) + \cos(\varphi_1 - \varphi_2) &= 2 \cdot \cos(\varphi_1) \cdot \cos(\varphi_2)\\[7pt]
\cos(\varphi_1 + \varphi_2) - \cos(\varphi_1 - \varphi_2) &= -2 \cdot \sin(\varphi_1) \cdot \sin(\varphi_2)
\end{aligned} $$
Formeln für Produkte von trigonometrischen Termen
$$ \begin{aligned}
\sin(\varphi_1) \cdot \sin(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\cos(\varphi_1-\varphi_2) - \cos(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\cos(\varphi_1) \cdot \cos(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\cos(\varphi_1-\varphi_2) + \cos(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\sin(\varphi_1) \cdot \cos(\varphi_2) &= \dfrac{1}{2} \cdot \Bigl[\sin(\varphi_1-\varphi_2) + \sin(\varphi_1 + \varphi_2)\Bigr]\\[7pt]
\sin(\varphi) \cdot \cos(\varphi) &= \dfrac{1}{2} \cdot \Bigl(\sin(2 \varphi)\Bigr)\\[7pt]
\tan(\varphi_1) \cdot \tan(\varphi_2) &= \dfrac{\tan(\varphi_1) + \tan(\varphi_2)}{\cot(\varphi_1) + \cot(\varphi_2)} = -\dfrac{\tan(\varphi_1) - \tan(\varphi_2)}{\cot(\varphi_1) - \cot(\varphi_2)}\\[7pt]
\cot(\varphi_1) \cdot \cot(\varphi_2) &= \dfrac{\cot(\varphi_1) + \cot(\varphi_2)}{\tan(\varphi_1) + \tan(\varphi_2)} = -\dfrac{\cot(\varphi_1) - \cot(\varphi_2)}{\tan(\varphi_1) - \tan(\varphi_2)}\\[7pt]
\tan(\varphi_1) \cdot \cot(\varphi_2) &= \dfrac{\tan(\varphi_1) + \cot(\varphi_2)}{\cot(\varphi_1) + \tan(\varphi_2)} = -\dfrac{\tan(\varphi_1) - \cot(\varphi_2)}{\cot(\varphi_1) - \tan(\varphi_2)}
\end{aligned} $$