Skip to main content Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Rigid Body Statics

Fundamentals: Are you ready to explore the world of rigid bodies?

In this chapter, we will dive into the fascinating world of rigid body mechanics and explore:

  • The invisible forces that act on objects and set them in motion or slow them down.
  • The secret of cutting free, which allows us to isolate the most important forces acting on an object.
  • The magical free body diagrams, which show us how forces and moments act on an object.
  • The rigid body and its six degrees of freedom, which give it its mobility.
  • The 6 axioms of rigid body statics, which are the foundation for everything we know about objects at rest.

Are you ready to uncover these secrets?

Then buckle up and let's go on an exciting journey into the world of rigid body mechanics!

It's going to be exciting!

On this Page
Table of Contents

1.1 The Force Vector

More than just mass times acceleration

Hey, do you know this? You're studying mechanics, you're lost in thought, and suddenly you push your tablet or smartphone on the table. Sometimes straight, sometimes at an angle. What happens? Exactly, it moves differently! Crazy, right?

Why is that?

Quite simply: Forces are defined not only by their magnitude but also by their direction and point of application.

Let's imagine your smartphone is a small bag filled with sand.

You push it several times with a force of the same magnitude:

  • If you push it vertically from above, nothing happens. The sack collapses and does not move.
  • But if you push it diagonally, it slides in one direction.
  • And if you grab it by the corner and pull, it might even tip over!

Do you understand? Forces are like invisible arrows. They have a direction and a point of application. And depending on how you push the small bag, it moves differently.

Okay, okay, but how does it work exactly?

Physicists call such a force arrow a force vector. It has three important properties:

  • Point of application: Where exactly you push the small bag.
  • Direction: Where you push, pull, push or lift it.
  • Magnitude (size): How hard you push it.
In a diagram, such a force vector looks like an arrow.
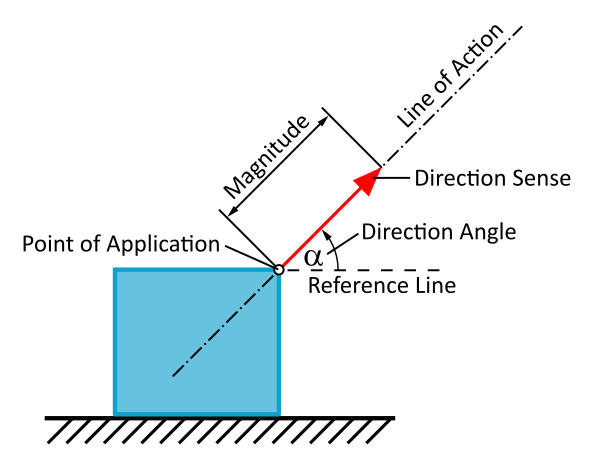
This Figure 2.1.1 shows a force vector with its characteristics.
Fig. 2.1.1: The Force Vector
  • The length of the arrow indicates the magnitude of the force - just note the scale (e.g. 1 cm ≙ 1 N).
  • The beginning of the arrow or the arrowhead (it doesn't really matter) indicates the point of application of the force vector.
  • To define the direction unambiguously, we need two things:
    • A direction angle, which is measured counterclockwise from a reference line. It leads to the line of action of the force. This is an imaginary line on which the force vector lies.
    • The direction sense on the line of action, represented by the arrowhead.
    In three-dimensional space it gets a bit more complicated. There you need not only one, but three direction angles. But don't worry, it's not that hard! Just imagine you are building a 3D coordinate system. With the three angles you can then order the force vector very precisely.
Isn't that so hard, is it?

With force vectors you can now understand all kinds of force effects. Whether it's pushing a box, throwing a ball or driving a car.

By the way: In physics, vectors are often represented by bold letters. So the force vector becomes F, the weight force becomes G and so on.

Sure, sometimes it's helpful to represent forces as arrows or bold letters. But most of the time it's enough to simply use the coordinates or magnitudes of the vectors.

Why? Because it's faster and easier! And besides: Our sketches and drawings show us anyway whether it is a vector.

So, don't panic! Vectors in engineering mechanics are easy.

Here's how it works:
  • Coordinates and magnitudes: Simply use the numbers to describe the force, e.g. \(F = \left(\begin{array}{c} 10~\mathrm{N} \\ 5~\mathrm{N} \\ 0~\mathrm{N} \end{array}\right)\) for a force in x-, y- and z-direction.
  • Sketches and drawings: A picture says more than a thousand words! Draw the force as an arrow and you know immediately where it comes from and where it goes.
  • Vector notation: Only when it is really important do we use the full vector power with arrows and bold letters.
So, that's enough physics for now.

Off to the outside and explore the world of engineering mechanics!

P.S.: And don't forget: Physics can also be fun!