Practice Exercise F-6.1.1
Area Moment of Inertia: Determine the Axial and Biaxial Area Moment of Inertia
Problem Statement
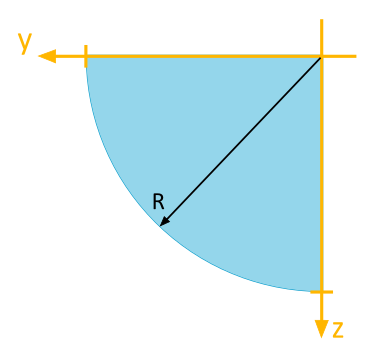
For the depicted quarter circle area, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
Short Solution
a) Determine the Axial Area Moment of Inertia \(I_y\)
$$ \begin{aligned}
I_y&= \dfrac{R^4 \pi}{16}
\end{aligned} $$
b) Determine the Axial Area Moment of Inertia \(I_z\)
$$ \begin{aligned}
I_z &= \dfrac{R^4 \pi}{16}
\end{aligned} $$
c) Determine the Biaxial Area Moment of Inertia \(I_{yz}\)
$$ \begin{aligned}
I_{yz} &= -\dfrac{1}{8}R^4
\end{aligned} $$
Comprehensive Solution
One approach to determine the area moment of inertia is to perform the calculation in Cartesian coordinates.
To minimize computational effort, we can avoid two double integrals. Therefore, it is advisable to use the following formulas in the calculation, based on the methods of horizontal and vertical infinitesimal area strips:
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.