Übungsaufgabe F-6.1.1 TechMech 2 Festigkeitslehre

Aufgabe F-6.1.1

Flächenträgheitsmoment: Axiales und Biaxiales Flächenträgheitsmoment bestimmen

Aufgabenstellung

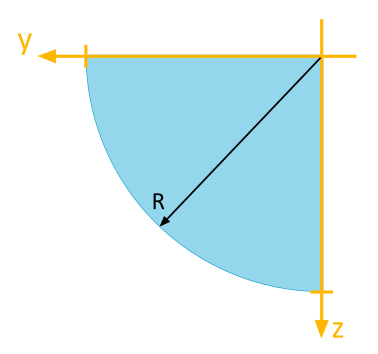
Viertelkreisfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Radius: R, Zentrum des Vollkreises: y,z, y nach links positiv, z nach unten positiv. — Abb. 1: Viertelkreis mit gegebenen Koordinatensystem

Für die abgebildete Viertelkreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Kurzlösung

a) Bestimme das axiale Flächenträgheitsmoment $I_y$

$$ \begin{aligned} I_y&= \dfrac{R^4 \pi}{16} \end{aligned} $$

b) Bestimme das axiale Flächenträgheitsmoment $I_z$

$$ \begin{aligned} I_z &= \dfrac{R^4 \pi}{16} \end{aligned} $$

c) Bestimme das biaxiale Flächenträgheitsmoment $I_{yz}$

$$ \begin{aligned} I_{yz} &= -\dfrac{1}{8}R^4 \end{aligned} $$

Ausführlicher Lösungsweg

Eine Möglichkeit zur Bestimmung der Flächenträgheitsmomente besteht darin, die Berechnung in kartesischen Koordinaten durchzuführen.

Wir können den Arbeitsaufwand möglichst gering halten, indem wir zwei Doppelintegrale vermeiden. Daher ist es empfehlenswert, bei der Berechnung die folgenden Formeln, basierend auf den Berechnungsmethoden horizontaler und vertikaler infinitesimaler Flächenstreifen, zu verwenden:

Weiterlesen mit TechMechAcademy+

Alles. Immer. Überall.

Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.

Werde ein TechMechAcademy+ Premiummitglied!

Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.