Practice Exercise in Mathematics for Engineers

Problem M-D-1.7

Differential Calculus: Tangent Line and Normal Line of Same Function

Problem Statement

Determine the points on the graph of

$$ f:x \mapsto f(x) = \frac{1}{x^2},~D_f = \mathbb{R} \setminus \{0\}$$

where the tangent line is also the normal line for the same curve. (The normal line is the perpendicular line to the tangent at the point of contact.)

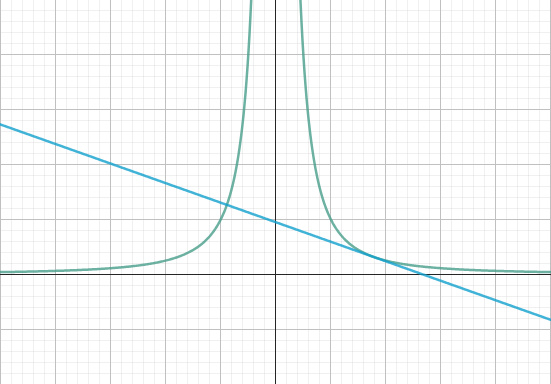
Function with tangent line — Fig. 1: Graph $f(x)=\frac{1}{x^2}$ and a Tangent Line which is also the normal line for the same curve

Short Solution

$$ \begin{align} &P_1~(-1.78,0.32)\\[7pt] &P_2~(1.78,0.32) \end{align} $$

Comprehensive Solution

Preliminary Considerations

We are looking for the points on the graph of $f(x)=\frac{1}{x^2}$ where the tangent is also the normal for the same curve.

To solve this task, we need to find the tangent equation for the function $f(x)$ in its general form. Afterward, we will search for the points of intersection between the tangent equations and the function $f(x)$. These points of intersection could potentially be where the tangent is also the normal for $f(x)$. We can calculate this by determining the slope of the normal at the intersection points and comparing it to the slope of the original tangent function.