Area Moment of Inertia - Definition

Introduction to the Area Moment of Inertia

Definition of the Axial Area Moment of Inertia

On this Page

Table of Contents

1.2. Definition

The area moment of inertia is also known as second moment of area. The second moment of area gets its name because it's a special type of moment. It is calculated by integrating the distance of an area from a reference line raised to the second power (as a square). The second moment of area is, therefore, a quantity derived from the geometric shape of the area itself.

We can illustrate this relationship using Figure 6.1.2:

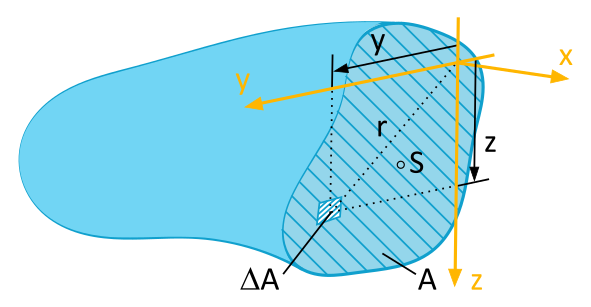
A surface element delta A is exemplarily represented within an arbitrary cross-sectional area. Its position is dimensioned based on an arbitrarily arranged yellow coordinate system with variables x, y, and z. The variables y, z, and r are used, where r represents the distance of the element from the origin of the coordinate system. — Fig. 6.1.2: Division of an arbitrary cross-sectional area into infinitely small area elements $\Delta A$

The concept of the order of moments originates from the mathematical theory of integration and is also used in engineering and physics. A moment of the $n$-th order is calculated by integrating the $n$-th power of the distance from the reference line. In the case of the second moment of area, the second power of the distance is integrated, hence the name moment of the second order.

To better understand this concept of the order of moments, let's first consider the definitions of zeroth and first-order area moments:

The zeroth-order area moment is the area of the cross-section:

$$ \begin{aligned} A &= \int\limits_{(A)} y^0 \ \mathrm{d}A = \int\limits_{(A)} z^0 \ \mathrm{d}A = \int\limits_{(A)} \ \mathrm{d}A \end{aligned} $$

The unit of the zeroth-order area moment is mm².

The first-order area moments are the static moments:

$$ \begin{alignat}{3} S_y &= \int\limits_{(A)} z \ \mathrm{d}A \qquad &&\text{First-order area moment with respect to the y-axis}\\[7pt] S_z &= \int\limits_{(A)} y \ \mathrm{d}A \qquad &&\text{First-order area moment with respect to the z-axis} \end{alignat} $$

(6.1)

The unit of the first-order area moment is mm³.

The static moment finds application in determining the centroid coordinates $y_s$ and $z_s$:

$$ \begin{aligned} y_s &= \dfrac{S_y}{A} = \dfrac{\int\limits_{(A)} z \ \mathrm{d}A}{A} \qquad \qquad z_s &= \dfrac{S_z}{A} = \dfrac{\int\limits_{(A)} y \ \mathrm{d}A}{A} \end{aligned} $$

The second moment of area describes the stiffness of a cross-sectional area, for example, in terms of bending, torsion, or buckling. Its unit is mm⁴.

The second moment of area or area moment of inertia is divided into four different area moments.

Mechanics of Materials

Topic: Area Moment of Inertia

1.2. Definition