Zum Hauptinhalt springen Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Festigkeitslehre / Elastostatik

Thema: Flächenträgheitsmoment

Hier erfährst du, was ein Flächenträgheitsmoment (auch: Flächenmoment 2. Grades oder Flächenmoment 2. Ordnung) ist, wo in der technischen Mechanik es Anwendung findet und wie es berechnet wird.

Lass uns gemeinsam diese wichtigen Konzepte erkunden.

Auf dieser Seite
Inhaltsverzeichnis

1.2. Definition

Das Flächenträgheitsmoment wird auch als Flächenmoment 2. Ordnung bezeichnet. Das Flächenmoment 2. Ordnung bekommt seinen Namen daher, das es eine spezielle Art von Moment ist. Es wird durch die Integration des Abstands einer Fläche von einer Bezugslinie in der zweiten Potenz (also als Quadrat) berechnet. Das Flächenmoment 2. Ordnung ist daher eine Größe, die aus der geometrischen Form der Fläche abgeleitet wird und eine Eigenschaft der Fläche selbst ist.

Wir verdeutlichen uns diesen Zusammenhang mithilfe der Abbildung 6.1.2:

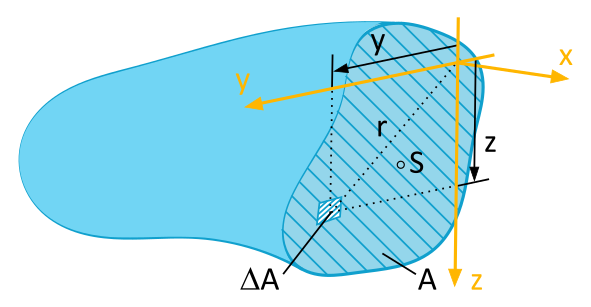
Ein Flächenelement delta A wird in einer beliebigen Querschnittsfläche exemplarisch dargestellt. Seine Position wird anhand eines beliebig angeordneten, gelben x,y,z-Koordinatensystems mit den Variablen y, z und r bemaßt, wobei r der Abstand des Elementes vom Ursprung des Koordinatensystems ist.
Abb. 6.1.2: Aufteilung einer beliebigen Querschnittsfläche in unendlich kleine Flächenelemente \(\Delta A\)

Das Konzept der Ordnung von Momenten stammt aus der mathematischen Theorie der Integration und wird auch in der Technik und Physik verwendet. Ein Moment der \(n\)-ten Ordnung wird durch die Integration der \(n\)-ten Potenz des Abstands von der Bezugslinie berechnet. Im Falle des Flächenmoments 2. Ordnung wird die zweite Potenz des Abstands integriert, daher die Bezeichnung als Moment 2. Ordnung.

Um uns dieses Konzept der Ordnung von Momenten zu verdeutlichen, betrachten wir zunächst die Definitionen der Flächenmomente 0. Ordnung und 1. Ordnung:

Das Flächenmoment 0. Ordnung ist die Fläche des Querschnitts:

$$ \begin{aligned} A &= \int\limits_{(A)} y^0 \ \mathrm{d}A = \int\limits_{(A)} z^0 \ \mathrm{d}A = \int\limits_{(A)} \ \mathrm{d}A \end{aligned} $$

Die Einheit des Flächenmomentes 0. Ordnung ist mm2.

Das Flächenmoment 1. Ordnung sind die statischen Momente

$$ \begin{alignat}{3} S_y&= \int\limits_{(A)} z \ \mathrm{d}A \qquad &&\text{Flächenmoment 1. Ordnung bezüglich der y-Achse}\\[7pt] S_z&= \int\limits_{(A)} y \ \mathrm{d}A \qquad &&\text{Flächenmoment 1. Ordnung bezüglich der z-Achse} \end{alignat} $$

(6.1)

Die Einheit des Flächenmomentes 1. Ordnung ist mm3.

Anwendung findet das statische Moment unter anderem bei der Bestimmung der Schwerpunktkoordinaten \(y_s\) und \(z_s\):

$$ \begin{aligned} y_s &= \dfrac{S_y}{A} = \dfrac{\int\limits_{(A)} z \ \mathrm{d}A}{A} \qquad \qquad z_s = \dfrac{S_z}{A} = \dfrac{\int\limits_{(A)} y \ \mathrm{d}A}{A} \end{aligned} $$

Das Flächenmoment 2. Ordnung beschreibt die Steifigkeit einer Querschnittsfläche z.B. in Bezug auf Biegung, Torsion oder Knickung. Seine Einheit ist mm4.

Man unterteilt das Flächenmoment 2. Ordnung bzw. Flächenträgheitsmoment in vier verschiedene Flächenmomente.