Zum Hauptinhalt springen Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Starrkörperstatik

Zentrale Kräftesysteme: Kräfte mit einem gemeinsamen Angriffspunkt

In der Technischen Mechanik spielt die Analyse von Kräften, die auf ein Objekt wirken, eine zentrale Rolle. Ein wichtiger Spezialfall ist das zentrale Kräftesystem, bei dem alle diese Kräfte einen gemeinsamen Angriffspunkt besitzen. In diesem Kapitel befassen wir uns mit den Eigenschaften und der Analyse zentraler Kräftesysteme und erkunden:

  • Definition und Eigenschaften: Was ist ein zentrales Kräftesystem? Welche besonderen Eigenschaften zeichnen es aus?
  • Grundaufgaben der Starrkörperstatik für zentrale Kräftesysteme:
    • Reduktion: Ein System von mehreren Kräften auf einen einzigen Punkt (Kraftschwerpunkt) reduzieren.
    • Gleichgewicht: Bestimmen, ob ein Körper unter der Wirkung von Kräften in Ruhe bleibt oder sich bewegt.
    • Zerlegung: Eine Kraft in mehrere Einzelkräfte zerlegen.

Bist du bereit, diese Geheimnisse zu lüften?

Auf dieser Seite
Inhaltsverzeichnis

1. Einführung

In der Technischen Mechanik spielt die Untersuchung von Kräften und ihren Auswirkungen auf Körper eine zentrale Rolle. Ein wichtiger Spezialfall dabei ist das zentrale Kräftesystem, bei dem mehrere Kräfte auf einen gemeinsamen Angriffspunkt wirken. In diesem Kapitel werden wir die Eigenschaften und Besonderheiten dieser Systeme genauer betrachten.

Definition und Eigenschaften

Ein zentrales Kräftesystem liegt vor, wenn alle Wirkungslinien der angreifenden Kräfte sich in einem Punkt schneiden.

Dieser Punkt wird als Zentralpunkt des Systems bezeichnet. Die Anzahl der Kräfte in einem solchen System kann beliebig sein, es muss jedoch mindestens eine Kraft vorhanden sein.

Wichtige Eigenschaften:
  • Translationsbewegung: Die resultierende Kraft eines zentralen Kräftesystems bewirkt immer eine Translationsbewegung des Körpers, d.h. eine geradlinige Bewegung ohne Drehung.
  • Momentenfreiheit: Da die Wirkungslinien aller Kräfte durch den Schwerpunkt verlaufen, ist das Gesamtdrehmoment des Systems gleich Null.
  • Vereinfachung der Analyse: Die Untersuchung eines zentralen Kräftesystems ist deutlich einfacher als die eines allgemeinen Kräftesystems, da nur die resultierende Kraft und der Schwerpunkt relevant sind.
Beispiel:

Stell dir vor, du hast eine Lampe, die an zwei Seilen hängt. Was passiert da? Welche Kräfte wirken? Und wie können wir das berechnen?

Diese Abbildung 3.1.1 zeigt eine Zimmerlampe, die über zwei Seile an der Decke aufgehängt ist.
Abb. 3.1.1: Balken mit Lampe

Zuerst schneiden wir die Lampe gedanklich an den Seilen vom Balken ab. So sehen wir die Reaktionskräfte F1 und F2 in den Seilen. Die Wirkungslinien dieser Kräfte verlaufen natürlich entlang der Seile und schneiden sich in einem Punkt P.

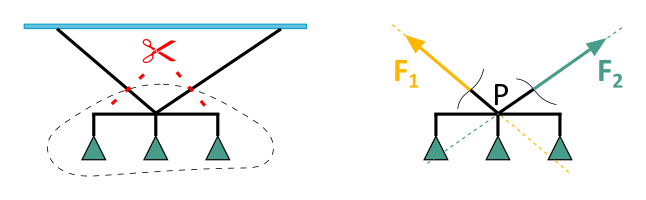
Diese Abbildung 3.1.2 zeigt den Freischnitt der Zimmerlampe.
Abb. 3.1.2: Freigeschnittene Lampe

Die Gewichtskraft der Lampe G wirkt ebenfalls durch diesen Punkt P. So haben wir ein zentrales Kräftesystem: Alle Wirkungslinien der Kräfte schneiden sich in einem Punkt.

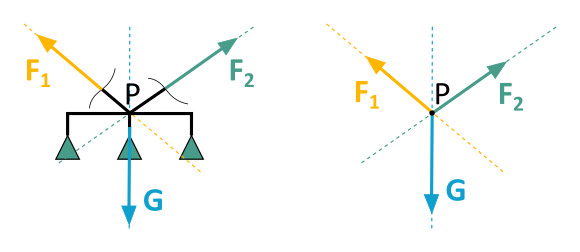
Diese Abbildung 3.1.3 zeigt das zentrale Kräftsystem an der Lampe.
Abb. 3.1.3: Lampe als zentrales Kräftesystem

Bis hier alles klar? Hier eine kurze Quizfrage zum Selbstcheck:

Warum werden die beiden Kräfte F1 und F2 jeweils nach schräg oben angenommen?

Beide müssen natürlich Zugkräfte sein, da Seile nur Zugkräfte in Richtung ihrer Längsachse aufnehmen können.

Die drei Grundaufgaben der Starrkörperstatik

Mit zentralen Kraftsystemen können wir drei wichtige Dinge machen:

  1. Reduktion auf eine Einzelkraft:

    Wir können alle Einzelkräfte zu einer einzigen Kraft zusammenfassen, der sogenannten Resultierenden. Das ist praktisch, wenn wir z.B. die Gesamtbelastung eines Bauteils berechnen wollen.

  2. Bedingungen für Gleichgewicht:

    Ein Körper ist im Gleichgewicht, wenn die Summe aller Kräfte und Momente gleich Null ist. Für zentrale Kraftsysteme bedeutet das: Die Resultierende muss gleich Null sein.

  3. Zerlegung einer Kraft:

    Wir können eine Kraft in zwei oder mehr andere Kräfte zerlegen. Das ist z.B. nützlich, wenn wir die Kräfte in den einzelnen Seilen der Lampe berechnen wollen.

Zeichnerische und rechnerische Untersuchung

Zentrale Kraftsysteme können wir sowohl zeichnerisch als auch rechnerisch untersuchen.

  1. Zeichnerisch:

    Mit Hilfe von Lage- und Kräfteplänen können wir die Kräfte grafisch darstellen und ihre Auswirkungen auf den Körper bestimmen.

  2. Rechnerisch:

    Mit Hilfe der Vektorrechnung können wir die Gleichungen der Statik lösen und die gesuchten Größen berechnen.

Zusammenfassung

Zentrale Kraftsysteme sind ein wichtiges Thema in der Statik. Mit den drei Grundaufgaben - Reduktion auf eine Einzelkraft, Bedingungen für Gleichgewicht und Zerlegung einer Kraft - können wir viele statische Probleme lösen.

Übrigens: Das zentrale Kräftesystem sind ein Spezialfall. Später lernen wir noch das allgemeine Kräftesystem kennen. Da wird es dann noch ein bisschen spannender.

So, genug Theorie! Jetzt ran an die Aufgaben!