Exercise F-1.2.1-xz TechMech 2 Mechanics of Materials

Practice Exercise F-1.2.1-xz

Plane Stress State: Arbitrary Section Angle, Coordinate Transformation x,z-Coordinate System

Problem Statement

In a sheet, the stresses $\sigma_x = -250\mathrm{~MPa}$, $\sigma_z = 80\mathrm{~MPa}$ and $\tau_{xz} = 50\mathrm{~MPa}$ are given.

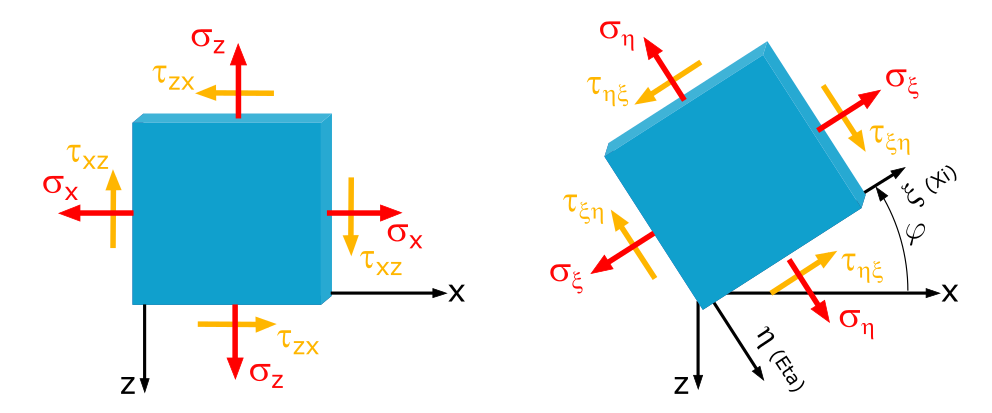
This illustration depicts a square sheet of metal in two positions. In one instance, it lies with two sides in an x, z-coordinate system with the origin at the bottom-left corner of the sheet. In the second position, it is tilted at an angle phi to the x-axis. The x-axis is positive to the right, and the z-axis is positive downward. Normal and shear stresses are represented for each side of the sheet, with arrows indicating their respective directions. — Fig. 1: Sheet with given stresses

What normal and shear stresses occur at a section angle of $\varphi=30°$?

Short Solution

What normal and shear stresses occur at a section angle of $\varphi=30°$?

$$ \begin{aligned} \sigma_\xi &= -210,801\mathrm{~MPa}~(\nearrow)\\ \sigma_\eta &= 40,801\mathrm{~MPa}~(\searrow)\\ \tau_{\xi\eta} &= -117,894\mathrm{~MPa}~(\searrow) \end{aligned} $$

Comprehensive Solution

For the given $x$, $z$-coordinate system, describing a plane where the x-axis points to the right in the positive direction and the z-axis points downward in the positive direction, and the given stresses $\sigma_x$, $\sigma_z$, and $\tau_{xz}$, we can use the formula 1.7_xz to determine the normal and shear stresses at any arbitrary angle $\varphi$:

Continue with TechMechAcademy+

Everything. Always. Everywhere.

With TechMechAcademy+ full access to all content.

Become a TechMechAcademy+ Premium Member!

Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.