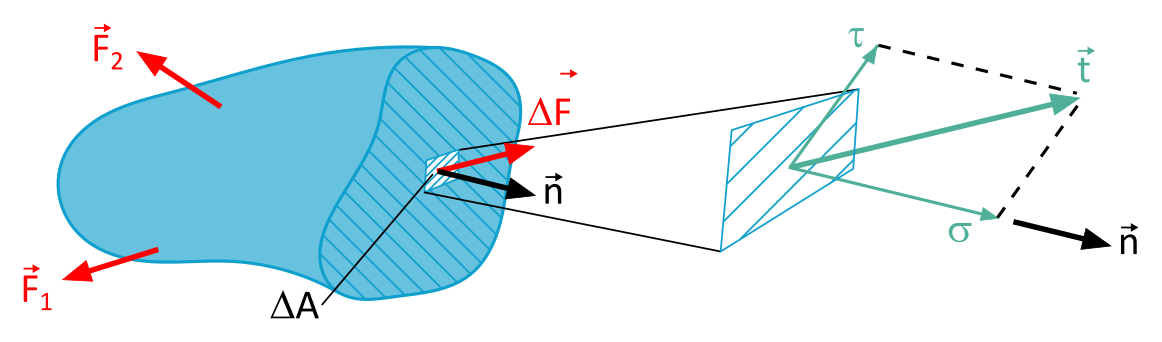
1.1 Stress Vector
Okay, okay, let's be honest, stress is not always as thrilling as in the movies. In reality, stress is far from evenly distributed. Imagine you are pressing on a piece of clay. The stress at the point where you press is obviously highest. But what about the edges? It's a completely different story there.
Therefore, it is simply not enough to calculate the average stress. Such a value tells you nothing about what it looks like at a specific point.
So let's grab a microscope and zoom in. We divide the area into many tiny subareas – so small that we can barely see them. A small force then acts on each of these tiny areas.
Now we can calculate the stress for each individual area element. And if we add up all these small stresses, we get a pretty accurate picture of the stress distribution in the entire area.
But wait a minute, there's something missing! Stress doesn't just have a magnitude, it also has a direction. In which direction does the force push?
That's exactly what the stress vector is for. It describes the stress at a specific point with magnitude and direction. It's like the sheriff in the wild west of stress.
Okay, okay, I know, formulas aren't everyone's cup of tea. But for the brave among you, here is the formula for the stress vector:
(1.1)
Don't worry, it's not as bad as it looks.
| Symbol | Description |
|---|---|
| \(\vec{t}\) | (mechanical) Stress vector |
| \(\Delta \vec{F}\) | Partial shear force transmitted in the surface element \(\Delta A\) |
| \(\Delta A\) | Surface element |
Okay, admittedly, the stress vector isn't the most exciting guy in the universe. But it's incredibly important for understanding how components work and how they can fail.
So, next time you see a building or a machine, remember: the stress vector is the invisible hero that holds it all together.