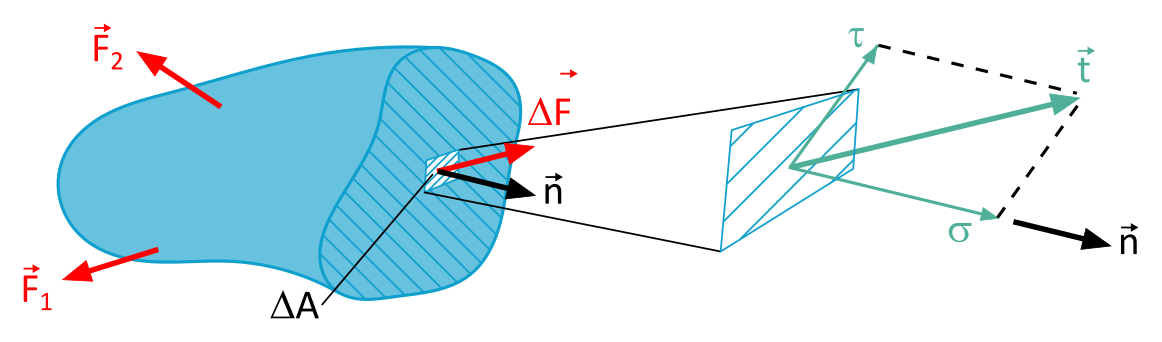
1.2 Components of the Stress Vector
Okay, okay, take a deep breath. It's actually not that bad. Imagine you have a piece of material and you want to know how the forces are distributed inside it. To do this, you imagine it being divided into many small surface elements. A stress vector acts on each of these elements.
But watch out: The stress vector \(\vec{t}\) is not always perpendicular to the surface you are investigating. Can you imagine that?
Therefore, we decompose the stress vector into two parts:
- Normal stress: The stress that is perpendicular to the surface. So to speak, the "compressive" or "tensile" force.
- Shear stress: The stress that acts parallel to the surface. So to speak, the "shearing" force.
Important: These two stresses depend on how you cut your piece of material. In other words, in which direction you place the cutting plane.
- Normal stress: Sigma (\(\sigma\)) – normally perpendicular, no need to guess.
- Shear stress: Tau (\(\tau\)) – shove that surface, feel the stress.
\(\vec{t} = \vec{\sigma} + \vec{\tau}\)
Don't worry if you're still a little confused. Stress vectors are a bit tricky at first. But with a little practice and this explanation, you'll soon understand them.
By the way: In Figure 1.1.2, you can see the decomposition of the stress vector in more detail: