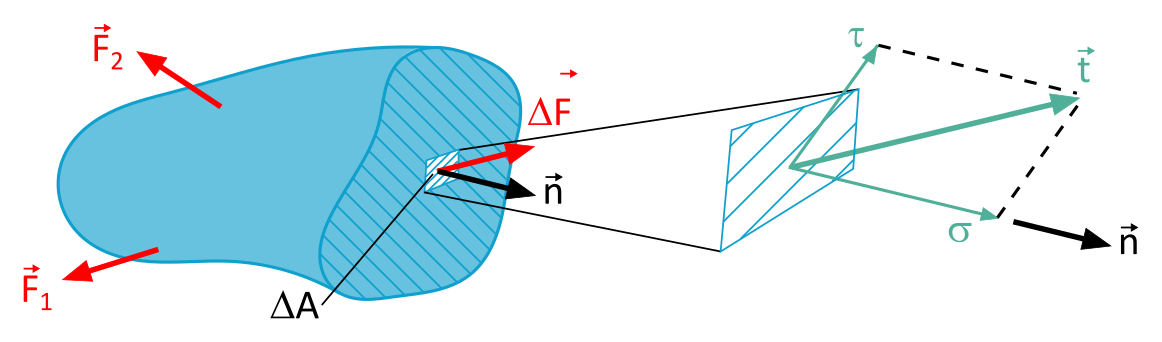
1.1 Spannungsvektor
Okay, okay, Spannungen sind ja nicht immer so prickelnd wie im Film. In der Realität sind sie meistens alles andere als gleichmäßig verteilt. Stell dir vor, du drückst auf ein Stück Knete. An der Stelle, wo du drückst, ist die Spannung natürlich am höchsten. Aber an den Rändern? Da sieht's ganz anders aus.
Deshalb reicht es einfach nicht, nur die mittlere Spannung zu berechnen. So ein Wert sagt dir nämlich nichts darüber, wie es an einem bestimmten Punkt aussieht.
Also schnappen wir uns ein Mikroskop und zoomen mal rein. Wir teilen die Fläche in ganz viele kleine Teilflächen – so klein, dass wir sie fast nicht mehr sehen können. Auf jeder dieser winzigen Flächen wirkt dann eine kleine Kraft.
Jetzt können wir die Spannung für jedes einzelne Flächenelement berechnen. Und wenn wir diese ganzen kleinen Spannungen zusammenaddieren, bekommen wir ein ziemlich genaues Bild von der Spannungsverteilung in der gesamten Fläche.
Aber Moment mal, da fehlt doch noch was! Spannung hat ja nicht nur eine Größe, sondern auch eine Richtung. In welche Richtung drückt die Kraft denn?
Genau dafür gibt's den Spannungsvektor. Er beschreibt die Spannung an einem bestimmten Punkt mit Größe und Richtung. Sozusagen der Sheriff im Wilden Westen der Spannungen.
Okay, okay, ich weiß, Formeln sind nicht jedermanns Sache. Aber für die ganz Mutigen unter euch gibt's hier noch die Formel für den Spannungsvektor:
(1.1)
Keine Angst, es ist nicht so schlimm, wie es aussieht.
| Zeichen | Größe |
|---|---|
| \(\vec{t}\) | (mechanischer) Spannungsvektor |
| \(\Delta \vec{F}\) | Im Flächenelement \(\Delta A\) übertragene Teilschnittkraft |
| \(\Delta A\) | Flächenelement |
Okay, zugegeben, der Spannungsvektor ist nicht der spannendste Typ im Universum. Aber er ist unglaublich wichtig, um zu verstehen, wie Bauteile funktionieren und wie sie kaputt gehen können.
Also, nächstes Mal, wenn du ein Gebäude oder eine Maschine siehst, denk dran: Der Spannungsvektor ist der unsichtbare Held, der alles zusammenhält.