1.2 Komponenten des Spannungsvektors
Okay, okay, atme tief durch. Es ist eigentlich gar nicht so schlimm. Stell dir vor, du hast ein Materialstück und willst wissen, wie die Kräfte darin verteilt sind. Dazu zerlegst du es in Gedanken in ganz viele kleine Flächenelemente. An jedem dieser Elemente wirkt ein Spannungsvektor.
Aber Achtung: Der Spannungsvektor \(\vec{t}\) steht nicht immer senkrecht auf der Fläche, auf die du untersuchst. Kannst du dir das vorstellen?
Deshalb zerlegen wir den Spannungsvektor in zwei Teile:
- Normalspannung: Die Spannung, die senkrecht auf der Fläche steht. Sozusagen die "quetschende" bzw. "ziehende" Kraft.
- Schubspannung: Die Spannung, die parallel zur Fläche wirkt. Sozusagen die "verschiebende" Kraft.
Wichtig: Diese beiden Spannungen hängen davon ab, wie du dein Stück Material schneidest. Also in welche Richtung du die Schnittebene legst.
- Normalspannung: Sigma (\(\sigma\)) – klingt wie "senkrecht"
- Schubspannung: Tau (\(\tau\)) – klingt wie "tangential"
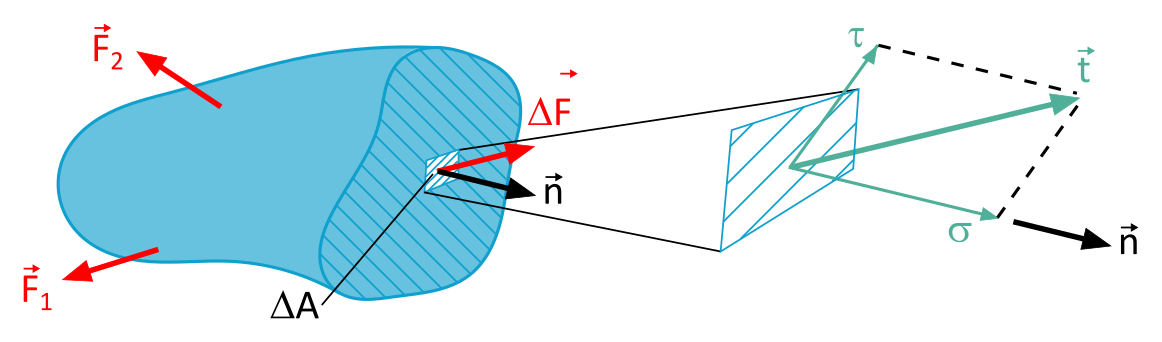
Merke dir: Den Spannungsvektor \(\vec{t}\) kannst du immer in zwei Teile zerlegen: die Normalspannung \(\sigma\) und die Schubspannung \(\tau\). Sozusagen die "Zutaten" des Spannungsvektors.
\(\vec{t} = \vec{\sigma} + \vec{\tau}\)
Keine Sorge, wenn du noch etwas verwirrt bist. Spannungsvektoren sind anfangs etwas tricky. Aber mit ein bisschen Übung und dieser Erklärung wirst du sie bald verstehen.
Übrigens: In der Abbildung 1.1.2 siehst du die Zerlegung des Spannungsvektors noch einmal ganz genau: