Reduction to a Single Force - Analytical Solution

First Basic Task: Reduction to a Single Force - Graphical Solution

Second Basic Task: Equilibrium - Graphical Solution

On this Page

Practice Exercises

Table of Contents

3. First Basic Task: Reduction to a Single Force

Analytical Solution

Okay, aspiring engineer, pay attention!

Remember the graphical method from the last chapter? As cool as it is in 2D, it is unfortunately not very accurate and impractical for 3D. That's why we're now going to flex our math skills and solve the problem in a precise and elegant way.

Grab your pen, paper, and your best buddy, the calculator, and let's get started!

What you need to know:

Forces are vectors:
$$ \begin{align} \tag{1} \vec{F} &= \begin{pmatrix} F_x\\ F_y \\ F_z \end{pmatrix} \end{align} $$
The resultant is the sum of all individual forces:
$$ \begin{align} \tag{2} \vec{R} &= \vec{F}_1 + \vec{F}_2 + \ldots + \vec{F}_n \end{align} $$
Vectors are added component-wise, so for example, the x-component of the resultant is:
$$ \begin{align} \tag{3} R_x &= {F_1}_x + {F_2}_x + \ldots + {F_n}_x = \sum_{i=1}^n {F_i}_x \end{align} $$
In 2D, you need the angle $\alpha$ from the positive x-axis to the force vector (counterclockwise positive) as well as the magnitude of each force.

Fig. 3.3.1: Force vector in the plane
In 3D, you need the three direction angles $\alpha_x$, $\alpha_y$ and $\alpha_z$, each measured from the positive coordinate axis of the desired force component to the force vector as well as the magnitude of each force.

Fig. 3.3.2: Force vector in space
You calculate the magnitude of a force vector:
- 2D:
  $$ \begin{align} \tag{4} F &= \sqrt{{F_x}^2 + {F_y}^2} \end{align} $$
- 3D:
  $$ \begin{align} \tag{5} F &= \sqrt{{F_x}^2 + {F_y}^2+ {F_z}^2} \end{align} $$
Often, the magnitude is given in the problem statement, e.g., F=10N.

How to calculate the resultant:

Step 1: Add the components of the individual forces:

2D:
$$ \begin{aligned} R_x &= \sum_{i=1}^n F_i \cdot \cos \alpha_i \\[12pt] R_y &= \sum_{i=1}^n F_i \cdot \sin \alpha_i \end{aligned} $$
3D:
$$ \begin{aligned} R_x &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_x \\[12pt] R_y &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_y \\[12pt] R_z &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_z \end{aligned} $$

(2.4)

Important: If you insert the angles as shown in Fig. 3.3.1 and Fig. 3.3.2 into equations (2.4), you get the components of the force vectors with the correct sign. So positive if the component acts in the direction of the coordinate system axis and negative if it acts against the direction of the axis.

By the way, in 3D, the counting direction of the angles $\alpha_x$, $\alpha_y$ and $\alpha_z$ does not matter. You measure the minimum angle between the positive coordinate axis of the component to be determined and the force vector.

Want to know why?

Very good! Take a look at the explanations of the trigonometric functions on the unit circle. Then you will understand why the sine is positive in the I. and II. quadrant of the coordinate system (positive y-axis) and the cosine is positive in the I. and IV. quadrant (positive x-axis) in 2D.

And take a look at the explanations of the cosine function. Then you will understand why it doesn't matter whether we calculate $\cos(\alpha)$ or $\cos(-\alpha)$ in 3D: We get the same result.

Step 2: Calculate the magnitude of the resultant:

2D:
$$ \begin{aligned} R = \sqrt{{R_x}^2 + {R_y}^2} \end{aligned} $$
3D:
$$ \begin{aligned} R &= \sqrt{{R_x}^2 + {R_y}^2+ {R_z}^2} \end{aligned} $$

(2.5)

Step 3: Determine the direction of the resultant:

2D:
$$ \begin{aligned} \alpha_R &= \arctan \dfrac{R_y}{R_x} \end{aligned} $$
3D:
$$ \begin{aligned} {\alpha_R}_x &= \arccos \dfrac{R_x}{R} \\[12pt] {\alpha_R}_y &= \arccos \dfrac{R_y}{R} \\[12pt] {\alpha_R}_z &= \arccos \dfrac{R_z}{R} \end{aligned} $$

(2.6)

Unfortunately, there is a tiny little problem with calculating the angle $\alpha_R$ using the tangent function:

The tangent function plays a bit of a trick on us because it's not unique between 0 and 360°.

But don't panic! With a little trickery, we can handle this. First, we calculate the acute angle ${\alpha_R}_{\text{acute}}$ using the arctangent function and the absolute values of the components, meaning we plug them in as positive values even if they are actually negative:

$$ \begin{align} \tag{6} {\alpha_R}_{\text{acute}} &= \arctan \dfrac{|R_y|}{|R_x|} \end{align} $$

This angle is always between 0° and 90°. Now we just need to find the correct quadrant where our $\alpha_R$ lies. For that, we take a look at the four cases in Figure 3.3.3:

This figure 3.3.3 shows a force vector R in the 4 different quadrants of the plane coordinate system. — Fig. 3.3.3: Four cases for determining the direction angle $\alpha_R$ of the resultant force R

With this, we can determine the direction angle $\alpha_R$ using the following table:

Case	$R_x$	$R_y$	$\alpha_R$
1	$>0$	$>0$	${\alpha_R}_{\text{acute}}$
2	$<0$	$>0$	$180° - {\alpha_R}_{\text{acute}}$
3	$<0$	$<0$	$180° + {\alpha_R}_{\text{acute}}$
4	$>0$	$<0$	$360° - {\alpha_R}_{\text{acute}}$

Tip:

Sketch the situation to better understand the direction of the resultant.

See, that wasn't so bad! With these tricks, you can master any reduction task.

And if you ever get stuck, no worries! In the practice exercises, we'll take a closer look at reducing central force systems.

Good luck!

Practice Exercises

Practice Exercise S-1.1.1

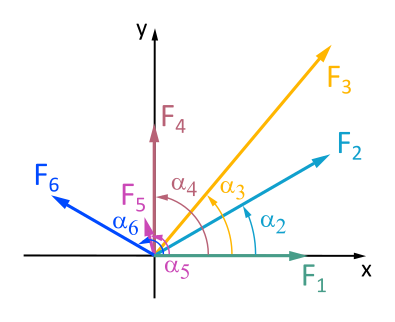
Graphically and analytically determine the magnitude and direction of the resultant force from forces F₁ to F₆.

$$ \begin{alignat}{5} F_1 &= 1000~\mathrm{N} \quad && \alpha_1 &&=0° \\[7pt] F_2 &= 1280~\mathrm{N} \quad && \alpha_2 &&=30° \\[7pt] F_3 &= 1750~\mathrm{N} \quad && \alpha_3 &&=50° \\[7pt] F_4 &= 840~\mathrm{N} \quad && \alpha_4 &&=90° \\[7pt] F_5 &= 220~\mathrm{N} \quad && \alpha_5 &&=100° \\[7pt] F_6 &= 760~\mathrm{N} \quad && \alpha_6 &&=150° \end{alignat} $$

Practice Exercise S-1.1.2

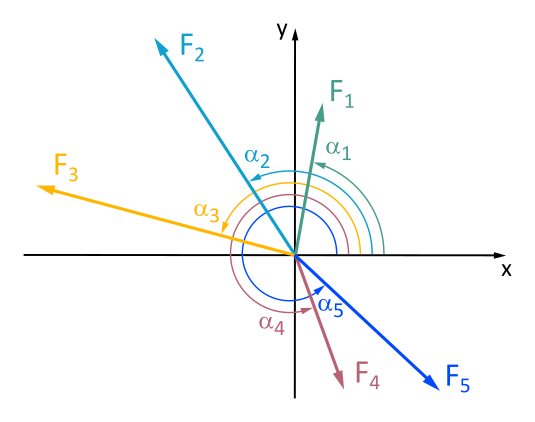
Graphically and analytically determine the magnitude and direction of the resultant force from forces F₁ to F₅.

$$ \begin{alignat}{5} F_1 &= 120~\mathrm{N} \quad && \alpha_1 &&=80° \\[7pt] F_2 &= 200~\mathrm{N} \quad && \alpha_2 &&=123° \\[7pt] F_3 &= 220~\mathrm{N} \quad && \alpha_3 &&=165° \\[7pt] F_4 &= 90~\mathrm{N} \quad && \alpha_4 &&=290° \\[7pt] F_5 &= 150~\mathrm{N} \quad && \alpha_5 &&=317° \end{alignat} $$

Practice Exercise S-1.1.3

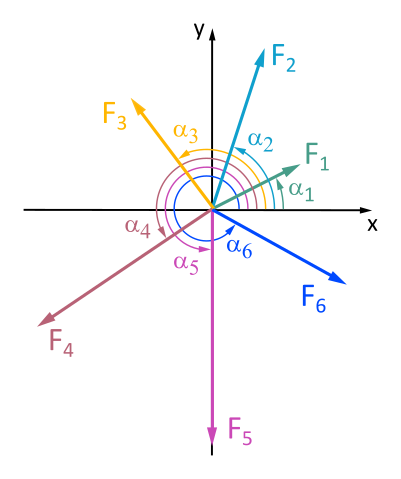
Graphically and analytically determine the magnitude and direction of the resultant force from forces F₁ to F₆.

$$ \begin{alignat}{5} F_1 &= 75~\mathrm{N} \quad && \alpha_1 &&=27° \\[7pt] F_2 &= 125~\mathrm{N} \quad && \alpha_2 &&=72° \\[7pt] F_3 &= 95~\mathrm{N} \quad && \alpha_3 &&=127° \\[7pt] F_4 &= 150~\mathrm{N} \quad && \alpha_4 &&=214° \\[7pt] F_5 &= 170~\mathrm{N} \quad && \alpha_5 &&=270° \\[7pt] F_6 &= 115~\mathrm{N} \quad && \alpha_6 &&=331° \end{alignat} $$

Practice Exercise S-1.1.4

Picture this: you've got two laundry lines, let's call them Line 1 and Line 2, that you need to attach to a wall. Imagine you're looking down at the setup from above. Something like this:

We know that the force acting on Line 1, which we'll call F₁, is 100 Newtons (N).

Determine the force F₂ acting on Line 2 in such a way that the combined force, or resultant force, is perpendicular to the wall.

Practice Exercise S-1.1.5

The traction rope of a conveyor system runs at an angle of $\gamma = 40°$ to the vertical from the pulley. Due to the mass of the conveyor basket, a rope force F₁ = 50 kN results.

What is the magnitude of the resultant of the two rope forces that act as bearing loads in pulley bearings A?
At what direction angle $\alpha_R$ (measured from the positive x-axis) does the resultant act?

Practice Exercise S-1.1.6

Four people are pulling a cart with ropes that are hooked into the towing eye of the drawbar according to the sketch.

Given:

F₁=400 N, F₂=350 N, F₃=300 N, F₄=500 N

Determine the magnitude of the resultant force R.
Determine the direction angle $\alpha_R$ of the resultant force relative to the horizontal line through the drawbar.

Case	\(R_x\)	\(R_y\)	\(\alpha_R\)
1	\(>0\)	\(>0\)	\({\alpha_R}_{\text{acute}}\)
2	\(<0\)	\(>0\)	\(180° - {\alpha_R}_{\text{acute}}\)
3	\(<0\)	\(<0\)	\(180° + {\alpha_R}_{\text{acute}}\)
4	\(>0\)	\(<0\)	\(360° - {\alpha_R}_{\text{acute}}\)

Rigid Body Statics

Central Force Systems: Forces with a Common Point of Application

3. First Basic Task: Reduction to a Single Force