3. Erste Grundaufgabe: Reduktion auf eine Einzelkraft
Erinnerst du dich an die grafische Methode aus dem letzten Kapitel? So cool sie in 2D auch ist, sie ist leider nicht sehr genau und für 3D ist sie einfach unpraktisch. Deswegen schwingen wir jetzt unsere Rechenkünste und lösen das Problem präzise und elegant.
Schnapp dir Stift, Zettel und deinen besten Kumpel, den Taschenrechner, und los geht's!
-
Kräfte sind Vektoren:
$$ \begin{align} \tag{1} \vec{F} &= \begin{pmatrix} F_x\\ F_y \\ F_z \end{pmatrix} \end{align} $$
-
Die Resultierende ist die Summe aller Einzelkräfte:
$$ \begin{align} \tag{2} \vec{R} &= \vec{F}_1 + \vec{F}_2 + \ldots + \vec{F}_n \end{align} $$
-
Vektoren werden komponentenweise addiert, so ist z.B. die x-Komponente der Resultierenden:
$$ \begin{align} \tag{3} R_x &= {F_1}_x + {F_2}_x + \ldots + {F_n}_x = \sum_{i=1}^n {F_i}_x \end{align} $$
-
In 2D brauchst du den Winkel \(\alpha\) von der positiven x-Achse zum Kraftvektor (gegen den Uhrzeigersinn positiv gezählt) sowie den Betrag jeder
Kraft.

Abb. 3.3.1: Kraftvektor in der Ebene -
In 3D brauchst du die drei Richtungswinkel \(\alpha_x\), \(\alpha_y\) und \(\alpha_z\), jeweils von der positiven Koordinatenachse der gesuchten Kraftkomponente zum
Kraftvektor gemessen sowie den Betrag jeder Kraft.

Abb. 3.3.2: Kraftvektor im Raum -
Den Betrag eines Kraftvektors berechnest du:
-
2D:
$$ \begin{align} \tag{4} F &= \sqrt{{F_x}^2 + {F_y}^2} \end{align} $$
-
3D:
$$ \begin{align} \tag{5} F &= \sqrt{{F_x}^2 + {F_y}^2+ {F_z}^2} \end{align} $$
Oft wird der Betrag in der Aufgabenstellung gegeben, z.B. F=10N.
-
2D:
-
2D:
$$ \begin{aligned} R_x &= \sum_{i=1}^n F_i \cdot \cos \alpha_i \\[12pt] R_y &= \sum_{i=1}^n F_i \cdot \sin \alpha_i \end{aligned} $$
-
3D:
$$ \begin{aligned} R_x &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_x \\[12pt] R_y &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_y \\[12pt] R_z &= \sum_{i=1}^n F_i \cdot \cos {\alpha_i}_z \end{aligned} $$
(2.4)
Wichtig: Wenn du die Winkel wie in Abb. 3.3.1 und Abb. 3.3.2 dargestellt in die Gleichungen (2.4) einsetzt, erhältst du die Komponenten der Kraftvektoren vorzeichenrichtig. Also positiv, wenn die Komponente in Achsenrichtung des Koordinatensystems wirkt und negativ, wenn sie entgegen der Achsenrichtung wirkt.
Dabei spielt in 3D die Zählrichtung der Winkel \(\alpha_x\), \(\alpha_y\) und \(\alpha_z\) übrigens keine Rolle. Du misst den minimalen Winkel zwischen der positiven Koordinatenachse der zu bestimmenden Komponente und dem Kraftvektor.
Sehr gut! Schau die die Erläuterungen zu den Winkelfunktionen am Einheitskreis an. Dann wirst du verstehen, warum in 2D der Sinus im I. und II. Quadranten des Koordinatensystems (positive y-Achse) und der Kosinus im I. und IV. Quadranten (positive x-Achse) positiv sind.
Und schau die die Erläuterungen zur Kosinusfunktion an. Dann wirst du verstehen, warum es egal ist, ob wir in 3D \(\cos(\alpha)\) oder \(\cos(-\alpha)\) rechnen: Es kommt das gleiche Ergebnis heraus.
-
2D:
$$ \begin{aligned} R = \sqrt{{R_x}^2 + {R_y}^2} \end{aligned} $$
-
3D:
$$ \begin{aligned} R &= \sqrt{{R_x}^2 + {R_y}^2+ {R_z}^2} \end{aligned} $$
(2.5)
-
2D:
$$ \begin{aligned} \alpha_R &= \arctan \dfrac{R_y}{R_x} \end{aligned} $$
-
3D:
$$ \begin{aligned} {\alpha_R}_x &= \arccos \dfrac{R_x}{R} \\[12pt] {\alpha_R}_y &= \arccos \dfrac{R_y}{R} \\[12pt] {\alpha_R}_z &= \arccos \dfrac{R_z}{R} \end{aligned} $$
(2.6)
Leider gibt es bei der Berechnung des Winkels \(\alpha_R\) über die Tangensfunktion ein klitzekleines Problem:
Die Tangensfunktion spielt etwas verrückt, da sie zwischen 0 und 360° nicht eindeutig ist.
Aber keine Panik! Mit ein bisschen Trickserei kriegen wir das hin. Zuerst berechnen wir den spitzen Winkel \({\alpha_R}_{\text{Spitz}}\) mit Hilfe der Arkustangensfunktion und der Beträge der Komponenten, d.h. wir setzen sie positiv ein, auch wenn sie eigentlich negativ sind:
Dieser Winkel liegt immer zwischen 0° und 90°. Jetzt müssen wir nur noch den richtigen Quadranten finden, in dem unser \(\alpha_R\) liegt. Dafür schauen wir uns die vier Fälle in Abbildung 3.3.3 an:

Damit können den Richtungswinkel \(\alpha_R\) mit Hilfe folgender Tabelle bestimmen:
| Fall | \(R_x\) | \(R_y\) | \(\alpha_R =\) |
|---|---|---|---|
| 1 | \(>0\) | \(>0\) | \({\alpha_R}_{\text{Spitz}}\) |
| 2 | \(<0\) | \(>0\) | \(180° - {\alpha_R}_{\text{Spitz}}\) |
| 3 | \(<0\) | \(<0\) | \(180° + {\alpha_R}_{\text{Spitz}}\) |
| 4 | \(>0\) | \(<0\) | \(360° - {\alpha_R}_{\text{Spitz}}\) |
- Skizziere die Situation, um die Richtung der Resultierenden besser zu verstehen.
So easy ist das! Mit diesen Tricks meisterst du jede Reduktionsaufgabe.
Solltest du mal festhängen, keine Panik! In den Übungsaufgaben werden wir die Reduktion von zentralen Kräftesystemen noch genauer betrachten.
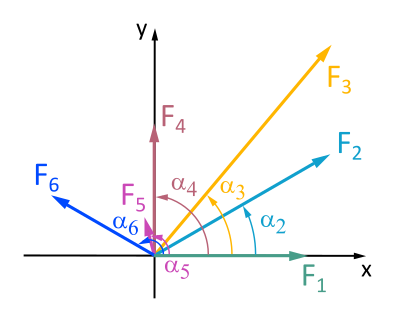
Ermittle grafisch und analytisch aus den Kräften F1 bis F6 den Betrag und die Richtung für die Resultierende.
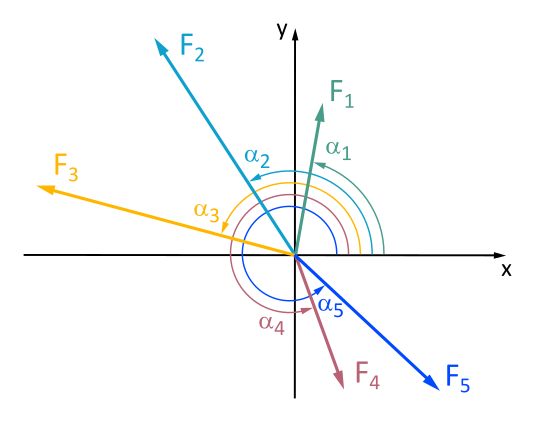
Ermittle grafisch und analytisch aus den Kräften F1 bis F5 den Betrag und die Richtung für die Resultierende.
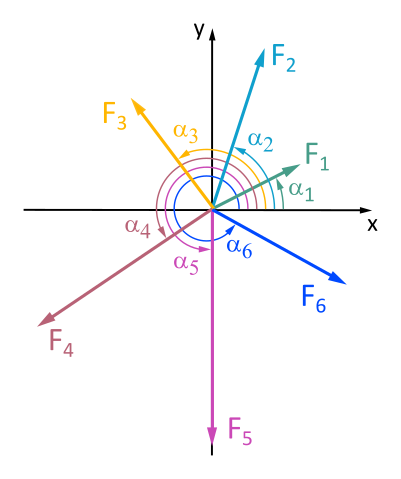
Ermittle grafisch und analytisch aus den Kräften F1 bis F6 den Betrag und die Richtung für die Resultierende.

Zwei Wäscheleinen (1 und 2) sollen an einer Wand befestigt werden. Die Skizze zeigt den Blick von oben.
Die Kraft F1 ist mit 100 N bekannt.
Bestimme F2 so, dass die Resultierende senkrecht zur Wand steht.

Das Zugseil einer Fördereinrichtung läuft unter \(\gamma = 40°\) zur Senkrechten von der Seilscheibe ab. Durch die Masse des Förderkorbes ergibt sich eine Seilkraft F1 = 50 kN.
- Welchen Betrag hat die Resultierende aus den beiden Seilzugkräften, die als Lagerbelastung in den Seilscheibenlagern A auftritt?
- Unter welchem Richtungswinkel \(\alpha_R\) (gemessen von der positiven x-Achse) wirkt die Resultierende?

Vier Personen ziehen einen Wagen an Seilen, die gemäß Skizze in die Zugöse der Deichsel eingehängt sind.
Gegeben:
F1=400 N, F2=350 N, F3=300 N, F4=500 N
- Bestimme den Betrag der resultierenden Kraft R.
- Bestimme den Richtungswinkel \(\alpha_R\) der Resultierenden zur horizontalen Linie durch die Deichsel.