Practice Exercise F-1.1.1
Uniaxial Stress State: Conical Rod and Compressive Force
Problem Statement
A conical rod with a circular cross-section and length \(l=250~\mathrm{mm}\) is loaded, as shown in Figure 1, by a compressive force \(F=10~\mathrm{kN}\) along the axis of the rod. The diameter at \(x=0\) is twice as large as the diameter at \(x=l\) with \(2d_0=150~\mathrm{mm}\) and \(d_0=75~\mathrm{mm}\), respectively.
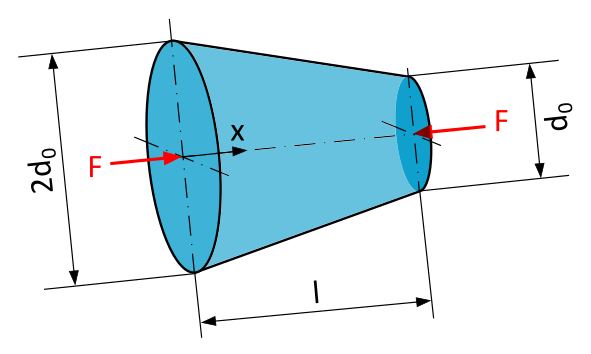
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the rod?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=200~\mathrm{mm}\) in a section perpendicular to the axis of the rod?
Short Solution
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the rod?
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the rod?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=200~\mathrm{mm}\) in a section perpendicular to the axis of the rod?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=200~\mathrm{mm}\) in a section perpendicular to the axis of the rod?
Comprehensive Solution
Considerations
The rod is loaded by a force \(F\) whose line of action is the axis of the rod. This means: We have a uniaxial stress state.
We are looking for the normal stress in a section perpendicular to the rod's axis. The general formula is:
(1.3)
The difficulty of this task lies in the fact that the cross-sectional area \(A\) of the rod is conical and therefore different for each position \(x\). Hence, \(A=A(x)\). Accordingly, we need formula 1.3b to solve this task:
(1.3b)
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the rod's axis?
Step 1: Determine Normal Force
Imagine cutting the rod at any point \(x\). At the intersection, two forces act, opposite and equal in magnitude: the normal force N in duplicate. This is the only way this intersection can be in equilibrium.
As a reminder: On the positive, left side of the cut, we apply \(N\) in a positive direction (towards the positive x-axis), while on the negative, right side of the cut, we apply it in a negative direction (against the positive x-axis).
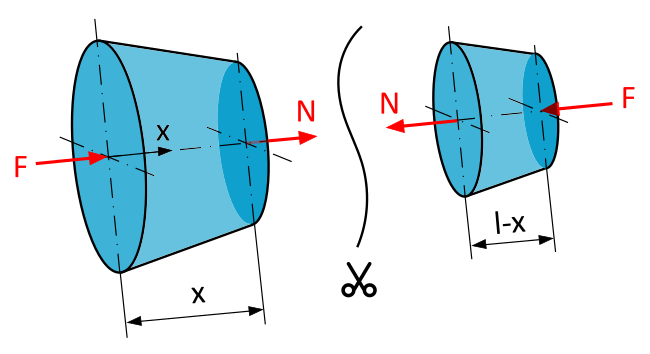
Since the rod is in equilibrium (i.e., it does not move), the forces in the x-direction must be equal.
If we apply the horizontal equilibrium condition for, say, our left cut, we can determine the normal force \(N\):
So: N = -F. This means that the normal force is negative because it counteracts the compressive force. It acts exactly opposite to how we have drawn it in Fig. 2.
Thus, we obtain a constant (independent of \(x\)), negative, internal normal force, i.e., we have a compressive force, and according to Equation 1.3/1.3b, a compressive stress. This must be the case, as the area is positive and negative force through positive area results in negative stress (= compressive stress).
Quite simply: At the beginning of the rod, an external force acts on our rod. Since there is no change in this force due to additional external forces until the end of the rod, the normal force remains constant over the entire rod.
Step 2: Determine Area as a Function of \(x\)
Since it is a conical rod, the cross-sectional area in the perpendicular cut to the axis of the rod is always circular. The formula for the area of a circle is:
As mentioned above, the difficulty of this task lies in the fact that the cross-sectional area \(A\) of the rod is conical and therefore varies for each position \(x\). When we examine the problem in a graph, we quickly realize that we need to represent the radius \(r\) as a function of the position \(x\) in order to solve this task.
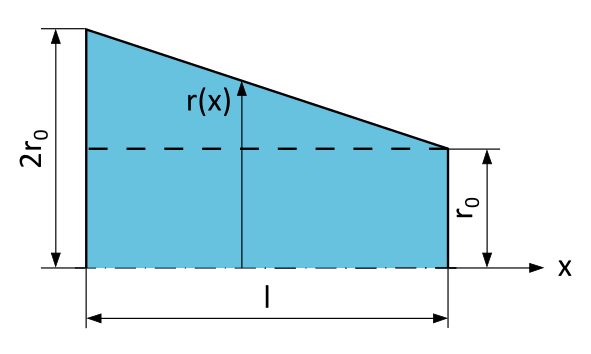
So we are looking for \(r(x)\) in order to describe the area as follows:
We can solve such a problem in at least two different ways. Either we apply the 2nd similarity theorem or we establish the functional equation of the line \(r(x)\).
Both approaches lead to the exact same result. The choice of which one to use depends on personal preference and familiarity. Therefore, let's take a closer look at both options.
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for working alongside the semester with the content of TechMechAcademy.
- Unrestricted admission to all content, both pre-existing and recently generated, within the scope of the premium membership.
- Guaranteed premium membership for three months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the third month from the start date. No cancellation necessary.
€29.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for semester preparation, concurrent semester work, and/or post-semester work with the content of TechMechAcademy.
- Unrestricted entry to a comprehensive collection of both existing and freshly generated content as part of the premium membership.
- Guaranteed premium membership for six months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the sixth month from the start date. No cancellation necessary.
€49.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.




