2.1 Normal Stress in Uniaxial Loading
Ditch the boring intro and dive straight into the action! Uniaxial loading? Think of a poor rod being stretched or squished by a mean force. That's it!
The poor rod gets deformed, and that's what we care about. It reveals how much stress is lurking inside the material.

Meet our hero: Normal stress. It describes the force per unit area acting on the poor rod.
- Positive force? It's tensile stress, pulling the rod like a taffy.
- Negative force? It's compressive stress, pushing the rod like a bully.
(1.3)
| Symbol | Name | Description | Unit |
|---|---|---|---|
| \(\sigma_x\) | Sigma | Normal stress in the x-direction | N/mm2 = MPa |
| \(N_x\) | Normal force in the x-direction | N | |
| \(F\) | Externally applied tensile or compressive force | N | |
| \(A\) | Area | mm2 |
- The force must be perpendicular to the area.
- The area must be the cross-sectional area of the rod.
Imagine a 10 cm2 rod with a 100 N load.
Each square centimeter of the rod is under 10 N of force. That's quite a lot, huh?
Relax, it's not here. The stress vector \(\vec{t}\) is perpendicular to the area, so the shear stress component is zero. No need to worry about it for now.
Things are about to get even more exciting! What happens when the force or the cross-sectional area isn't constant?
The stress isn't constant either! Take a hanging cone for example.

Where is the stress in the hanging cone smallest?
- At the pointy tip
- At the big, round top
- Neither
The answer is 1, of course! The stress is smallest at the pointy tip.
It's not because the cross-sectional area is smallest there. It's because there's no force acting at the tip! The cone hangs from the top, so the entire weight pulls down on the top area. The further down you go, the smaller the pulling force. And where there's no force, there's no stress!
In our cone, the normal force and the diameter change depending on the location. So the stress also changes:
(1.3b)
Uniaxial loading is a breeze! With a bit of math and imagination, you can calculate the stress in any material.
Study the example and test your knowledge! Calculate the stress in a rod of your choice. Have fun!
Example 1.1: Tapered Rod
A conical rod with a circular cross-section and length \(l = 250~\mathrm{mm}\) is loaded as depicted in Figure E1 by a compressive force \(F=10~\mathrm{kN}\) along the axis of the rod. The diameter at \(x=0\) is twice as large as the diameter at \(x=l\) with \(2d_0 = 150~\mathrm{mm}\) and \(d_0 = 75~\mathrm{mm}\), respectively.
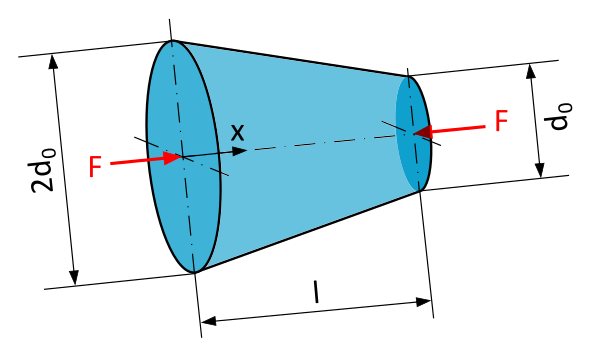
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the rod's axis?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=200~\mathrm{mm}\) in a section perpendicular to the rod's axis?
Solution
Considerations
The rod is loaded by a force \(F\) whose line of action is the axis of the rod. This means: We have a uniaxial stress state.
We are looking for the normal stress in a section perpendicular to the rod's axis. The general formula is:
(1.3)
The difficulty of this task lies in the fact that the cross-sectional area \(A\) of the rod is conical and therefore different for each position \(x\). Hence, \(A=A(x)\). Accordingly, we need formula 1.3b to solve this task:
(1.3b)
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the rod's axis?
Step 1: Determine Normal Force
Imagine cutting the rod at any point \(x\). At the intersection, two forces act, opposite and equal in magnitude: the normal force N in duplicate. This is the only way this intersection can be in equilibrium.
As a reminder: On the positive, left side of the cut, we apply \(N\) in a positive direction (towards the positive x-axis), while on the negative, right side of the cut, we apply it in a negative direction (against the positive x-axis).
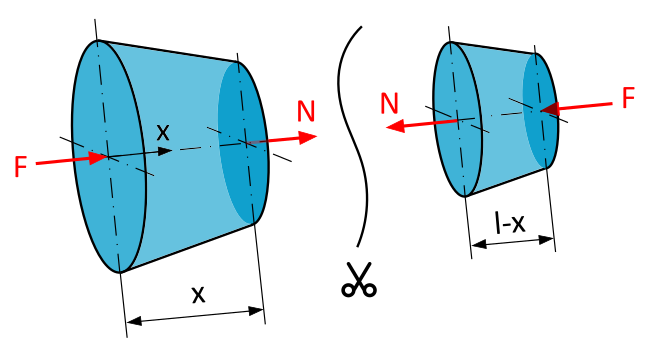
Since the rod is in equilibrium (i.e., it does not move), the forces in the x-direction must be equal.
If we apply the horizontal equilibrium condition for, say, our left cut, we can determine the normal force \(N\):
So: N = -F. This means that the normal force is negative because it counteracts the compressive force. It acts exactly opposite to how we have drawn it in Fig. E2.
Thus, we obtain a constant (independent of \(x\)), negative, internal normal force, i.e., we have a compressive force, and according to Equation 1.3/1.3b, a compressive stress. This must be the case, as the area is positive and negative force through positive area results in negative stress (= compressive stress).
Quite simply: At the beginning of the rod, an external force acts on our rod. Since there is no change in this force due to additional external forces until the end of the rod, the normal force remains constant over the entire rod.
Step 2: Determine Area as a Function of \(x\)
Since it is a conical rod, the cross-sectional area in the perpendicular cut to the axis of the rod is always circular. The formula for the area of a circle is:
As mentioned above, the difficulty of this task lies in the fact that the cross-sectional area \(A\) of the rod is conical and therefore varies for each position \(x\). When we examine the problem in a graph, we quickly realize that we need to represent the radius \(r\) as a function of the position \(x\) in order to solve this task.
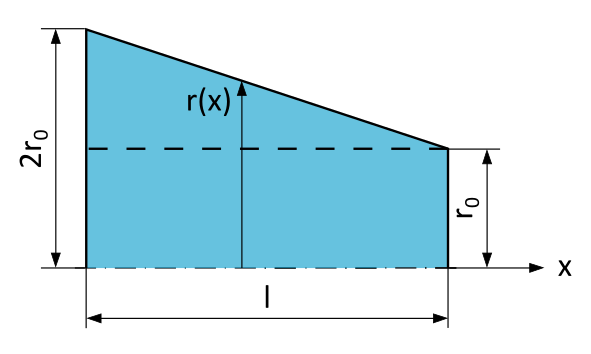
So we are looking for \(r(x)\) in order to describe the area as follows:
We can solve such a problem in at least two different ways. Either we apply the 2nd similarity theorem or we establish the functional equation of the line \(r(x)\).
Both approaches lead to the exact same result. The choice of which one to use depends on personal preference and familiarity. Therefore, let's take a closer look at both options.
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.
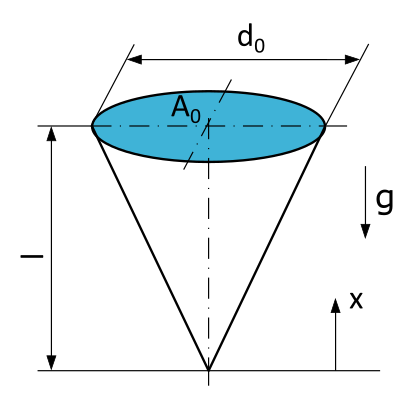
Suspended Cone
An icicle is hanging from a gutter. The icicle has the shape of a circular cone with a length \(l=10~\mathrm{cm}\), a diameter \(d_0=5~\mathrm{cm}\) at the suspension point, and a cross-sectional area \(A_0\). The ice has a density of \(\varrho = 0,91~\mathrm{g/cm^3}\).
- What is the formula for calculating the normal force \(N\) at any location x in a section perpendicular to the axis of the cone?
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the cone?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=70~\mathrm{mm}\) in a section perpendicular to the axis of the cone?
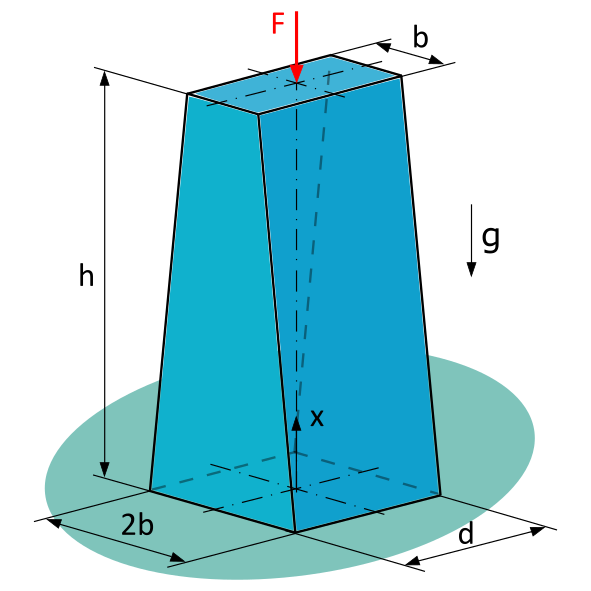
A Loaded Homogeneous Bar with Constant Thickness and Linearly Variable Width
A homogeneous bar with constant thickness \(d=20~\mathrm{mm}\) and linearly varying width is subjected to a compressive force \(F=1~\mathrm{kN}\).
Given: \(b=15~\mathrm{mm}\), \(h=80~\mathrm{mm}\), \(\varrho = 7,85~\mathrm{g/cm^3}\)
- What is the formula for calculating the cross-sectional area \(A(x)\) at any location x in a section perpendicular to the axis of the rod?
- What is the formula for calculating the normal force \(N(x)\) at any location x in a section perpendicular to the axis of the rod?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=30~\mathrm{mm}\) in a section perpendicular to the axis of the rod?


