Practice Exercise F-1.1.2
Uniaxial Stress State: Suspended Cone
Problem Statement
An icicle is hanging from a gutter. The icicle has the shape of a circular cone with a length \(l=10~\mathrm{cm}\), a diameter \(d_0=5~\mathrm{cm}\) at the suspension point, and a cross-sectional area \(A_0\). The ice has a density of \(\varrho = 0,91~\mathrm{g/cm^3}\).
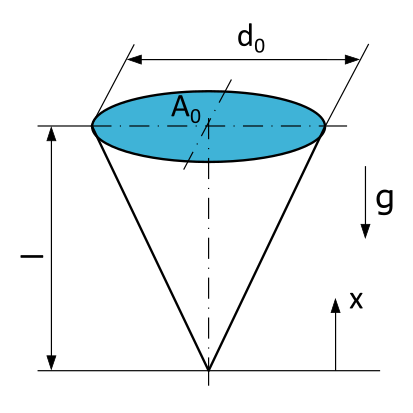
- What is the formula for calculating the normal force \(N\) at any location x in a section perpendicular to the axis of the cone?
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the cone?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=70~\mathrm{mm}\) in a section perpendicular to the axis of the cone?
Short Solution
- What is the formula for calculating the normal force \(N\) at any location x in a section perpendicular to the axis of the cone?
- What is the formula for calculating the normal force \(N\) at any location x in a section perpendicular to the axis of the cone?
If desired, one can further simplify \(r_0^2 \cdot \pi=A_0\) and obtain the final result as follows:
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the cone?
- What is the formula for calculating the normal stress \(\sigma\) at any location x in a section perpendicular to the axis of the cone?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=70~\mathrm{mm}\) in a section perpendicular to the axis of the cone?
- What is the magnitude of the normal stress \(\sigma\) at the location \(x=70~\mathrm{mm}\) in a section perpendicular to the axis of the cone?
Comprehensive Solution
Preliminary Considerations
So, you want to crack the stress state in the cone? Cool stuff! But don't worry, it's not as tough as it seems.
First things first: Chill out! The cone is sturdily hanging in there; it won't just tumble down. While gravity is pulling downward, the support reaction, that is, the gutter-icicle connection, holds its ground. This creates a uniaxial stress state – all chill, no stress.
Now, you're looking for the normal stress in a section perpendicular to the axis. For that, you need the formula:
(1.3)
Okay, okay, looks complicated, but it's not a big deal.
\(N_x\) is the normal force acting in the section. It depends on the weight force of the cut cone. And that, my friend, depends on the position x in the cone: The higher you cut, the more cone mass pulls downward, the greater \(N_x\).
\(A\) is the cross-sectional area of the cone at point \(x\). The higher you cut, the bigger the circle, the larger \(A\).
See, both \(N_x\) and \(A\) change with \(x\). That's why you need to use formula 1.3b to calculate stress at every point \(x\).
(1.3b)
But no need to panic! With a bit of math and patience, you got this.
Tip: Imagine slicing the cone into lots of thin discs. Calculate stress for each disc, and you'll get a sense of how stress is distributed in the cone.
Good luck! And if you ever feel stuck, just peek at the complete solution below.
P.S.: Don't forget that the cone is made of a certain material. The material influences stress, so consider the material properties.
P.P.S.: Oh, and units! Be careful with the right units; otherwise, the result won't add up in the end.
- What is the formula for calculating the normal force \(N\) at any location x in a section perpendicular to the axis of the cone?
Step 1: Determine the normal force \(N(x)\) based on the equilibrium conditions
To calculate the normal force, we cut the rod at any arbitrary point \(x\) and represent the external force \(F_G\) and the internal normal force \(N\).
As a reminder, at the positive left cross-section, we represent \(N\) in the positive direction (towards the positive x-axis), while at the negative right cross-section, we represent it in the negative direction (opposite to the positive x-axis).
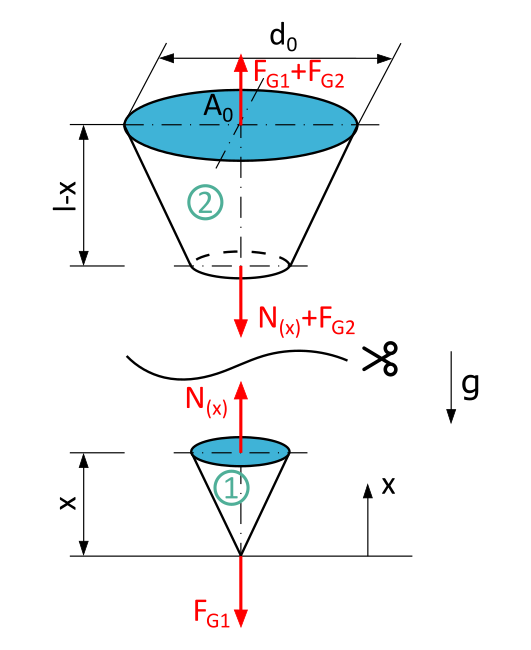
In this task, we need to consider that the weight of the "cut-off" cone-shaped object depends on \(x\): The larger the cut-off cone-shaped object, the greater its weight (here: \(F_{G1})\).
To solve this task, it is actually not necessary to cut out the remaining frustum of the cone from the section. But for the sake of completeness: At the right cross-section of the frustum, there are two forces acting: the reaction normal force of the section (also denoted as \(N(x)\)) and the weight of the remaining frustum (here: \(F_{G2})\).
In contrast, there is the reaction force of the gutter, which must be equal to the weight of the entire cone-shaped object before the section. This is because only this force acts as an external load, and the icicle must be in a state of rest.
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for working alongside the semester with the content of TechMechAcademy.
- Unrestricted admission to all content, both pre-existing and recently generated, within the scope of the premium membership.
- Guaranteed premium membership for three months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the third month from the start date. No cancellation necessary.
€29.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for semester preparation, concurrent semester work, and/or post-semester work with the content of TechMechAcademy.
- Unrestricted entry to a comprehensive collection of both existing and freshly generated content as part of the premium membership.
- Guaranteed premium membership for six months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the sixth month from the start date. No cancellation necessary.
€49.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.




