Practice Exercise F-6.2.1
Area Moment of Inertia: Determine Area Moments of Inertia for a Coordinate System Parallel to the Principal Axis System
Problem Statement
For the depicted rectangle, the following area moments of inertia with respect to the illustrated \(\overline{y}\), \(\overline{z}\)-coordinate system are to be determined:
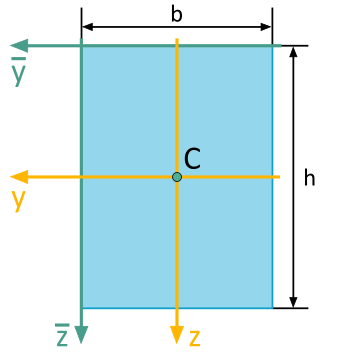
- Axial Second Moment of Inertia \(I_\overline{y}\)
- Axial Second Moment of Inertia \(I_\overline{z}\)
- Biaxial Second Moment of Inertia \(I_{\overline{yz}}\)
The area moments of inertia with respect to the principal axes are given as follows:
$$ \begin{align}
I_y &= \dfrac{b \cdot h^3}{12} \\[7pt]
I_z &= \dfrac{b^3 \cdot h}{12} \\[7pt]
I_{yz} &= 0
\end{align} $$
Short Solution
a) Determine the Axial Area Moment of Inertia \(I_\overline{y}\)
$$ \begin{aligned}
I_{\overline{y}} &= \dfrac{b \cdot h^3}{3}
\end{aligned} $$
b) Determine the Axial Area Moment of Inertia \(I_\overline{z}\)
$$ \begin{aligned}
I_{\overline{z}} &= \dfrac{b^3 \cdot h}{3}
\end{aligned} $$
c) Determine the Biaxial Area Moment of Inertia \(I_{\overline{yz}}\)
$$ \begin{aligned}
I_{\overline{yz}} &= \dfrac{b^2h^2}{4}
\end{aligned} $$
Comprehensive Solution
The reference axes of the sought area moments of inertia, \(\overline{y}\) and \(\overline{z}\), are parallel to the principal axes \(y\) and \(z\), for which the second-order area moments are known. Therefore, we need to apply formula (6.10) to solve this task with minimal effort:
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.