Exercise F-6.2.2 TechMech 2 - Mechanics of Materials

Practice Exercise F-6.2.2

Area Moment of Inertia: Determine Area Moment of Inertia for a Coordinate System Parallel to the Principal Axis System

Problem Statement

The depicted rectangular cross-section has an area of $A=72~\mathrm{cm}^2$.

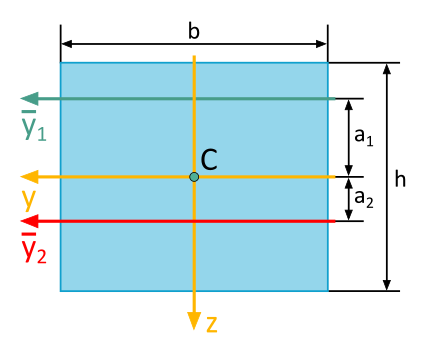
The illustration shows a rectangular cross-sectional area with a width of b and a height of h. A yellow y, z-coordinate system has its origin at the centroid of the area. A green y-bar-subscript-1 axis is located at a-subscript-1 distance above the yellow y-axis. A red y-bar-subscript-2 axis is located at a-subscript-2 distance below the yellow y-axis. The y-axes are positive to the left, and the z-axis is positive downward. — Fig. 1: Rectangular Surface

The axial area moment of inertia with respect to the $\overline{y}_1$-axis ($a_1 = 5~\mathrm{cm}$) is known and is $I_{\overline{y}_1}=2664~\mathrm{cm}^4$.

Calculate the axial area moment of inertia $I_{\overline{y}_2}$ with respect to the $\overline{y}_2$-axis ($a_2 = 2~\mathrm{cm}$).

Short Solution

$$ \begin{aligned} I_{\overline{y}_2} &= 1152~\mathrm{cm}^4 \end{aligned} $$

Comprehensive Solution

The reference axis of the sought area moment of inertia, $\overline{y}_2$, is parallel to the reference axis of the given area moment of inertia, $\overline{y}_1$.

However, a direct conversion of the given area moment of inertia $I_{\overline{y}_1}$ to the $\overline{y}_2$ axis using the Steiner's theorem according to Formula (6.10) is not permissible, as a fundamental prerequisite for the application of this formula is missing: Neither of the two axes, $\overline{y}_1$ and $\overline{y}_2$, is the centroid axis of the given rectangular area.

When the area moment of inertia, as in this case, needs to be converted from any axis to another parallel axis, i.e., both axes are not centroid axes, then two steps are necessary:

Continue with TechMechAcademy+

Everything. Always. Everywhere.

With TechMechAcademy+ full access to all content.

For Beginners: TechMechAcademy+. Full access to all content for one day.

Overview of the benefits:

Most cost-effective offer.
Ideal if you need access to already identified content for a short period.
Unlimited access to all existing and newly created content throughout the entire premium membership.
Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.

€3.99

TechMechAcademy+. Full access to all content for one week.

Overview of the benefits:

Cost-effective offer.
Ideal for short-term exam preparation with the content of TechMechAcademy.
Unlimited access to all existing and newly created content throughout the entire premium membership.
Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.

€9.99

Bestseller: TechMechAcademy+. Full access to all content for one month.

Overview of the benefits:

Benefit from the bestseller.
Ideal for effective exam preparation with the content of TechMechAcademy.
Unlimited access to all existing and newly created content throughout the entire premium membership.
Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.

€14.99

Become a TechMechAcademy+ Premium Member!

Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.