Übungsaufgabe F-6.2.2 TechMech 2 Festigkeitslehre

Aufgabe F-6.2.2

Flächenträgheitsmoment: Bestimme Flächenträgheitsmoment für ein Koordinatensystem parallel zum Schwerachsensystem

Aufgabenstellung

Der dargestellte Rechteckquerschnitt hat eine Fläche von $A=72~\mathrm{cm}^2$.

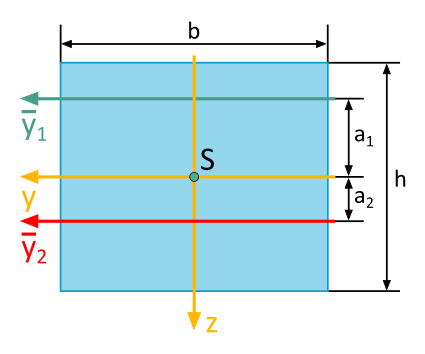
Die Abbildung zeigt eine rechteckige Querchnittsfläche mit der Breite b und der Höhe h. Ein gelbes y,z-Koordinatensystem hat seinen Ursprung im Schwerpunkt der Fläche. Eine grüne y mit Überstrich Index 1-Achse befindet sich im Abstand a Index 1 parallel über der gelben y-Achse. Eine rote y mit Überstrich Index 2-Achse befindet sich im Abstand a Index 2 parallel unter der gelben y-Achse. Die y-Achsen sind nach links positiv, die z-Achse nach unten positiv. — Abb. 1: Rechteckfläche

Das axiale Flächenträgheitsmoment bezogen auf die $\overline{y}_1$-Achse ($a_1 = 5~\mathrm{cm}$) ist bekannt und beträgt $I_{\overline{y}_1}=2664~\mathrm{cm}^4$.

Berechne das axiale Flächenträgheitsmoment $I_{\overline{y}_2}$ bezogen auf die $\overline{y}_2$-Achse ($a_2 = 2~\mathrm{cm}$).

Kurzlösung

$$ \begin{aligned} I_{\overline{y}_2} &= 1152~\mathrm{cm}^4 \end{aligned} $$

Ausführlicher Lösungsweg

Die Bezugachse des gesuchten Flächenträgheitsmomentes, $\overline{y}_2$, liegt parallel zur Bezugachse des gegebenen Flächenträgheitsmomentes, $\overline{y}_1$.

Dennoch ist eine direkte Umrechnung des gegebenen Flächenträgheitomentes $I_{\overline{y}_1}$ auf die $\overline{y}_2$-Achse mithilfe des Satzes von Steiner nach Formel (6.10) nicht zulässig, da eine grundlegende Voraussetzung zur Anwendung dieser Formel fehlt: Keine der beiden Achsen $\overline{y}_1$ und $\overline{y}_2$ ist Schwerpunktachse der gegebenen Rechteckfläche.

Muss das Flächenträgheitsmoment, wie in diesem Fall, von einer beliebigen Achse zu einer anderen beliebigen parallelen Achse umgerechnet werden, d.h. beide Achsen sind keine Schwerachsen, dann sind zwei Schritte notwendig:

Weiterlesen mit TechMechAcademy+

Alles. Immer. Überall.

Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.

Für Einsteiger: TechMechAcademy+. Voller Zugriff auf alle Inhalte für einen Tag.

Die Vorteile im Überblick:

Kostengünstigstes Angebot.
Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.

3,99 €

TechMechAcademy+. Voller Zugriff auf alle Inhalte für eine Woche.

Die Vorteile im Überblick:

Kostengünstiges Angebot.
Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.

9,99 €

Bestseller: TechMechAcademy+. Voller Zugriff auf alle Inhalte für einen Monat.

Die Vorteile im Überblick:

Profitiere vom Bestseller.
Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.

14,99 €

Werde ein TechMechAcademy+ Premiummitglied!

Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.