Skip to main content Skip to page footer
TechMechAcademy logo TechMechAcademy logo

Mechanics of Materials

Topic: Area Moment of Inertia

Here, you can learn what an area moment of inertia (also known as second moment of area, or second-order area moment) is, where it finds application in engineering mechanics, and how to calculate it.

Let's explore these essential concepts together.

On this Page
Table of Contents

1.2.3 Definition of the Biaxial Area Moment of Inertia

The biaxial area moment of inertia (also called the deviational moment or centrifugal moment) is a geometric quantity used in engineering mechanics when an asymmetric beam cross-section is subjected to pure bending or when an asymmetric load (a specific type of skew bending) occurs.

In such cases, the biaxial area moment of inertia is important as it accounts for the cross-section's inertia against a bending load acting in two directions, not just around the \(y\)- or \(z\)-axis.

$$ \begin{alignat}{3} I_{yz} &= I_{zy} = -\int\limits_{(A)} y \cdot z \ \mathrm{d}A \end{alignat} $$

(6.4)

Since the distances \(y\) and \(z\) of the infinitesimal area element \(\mathrm{d}A\) to the origin of the \(y\),\(z\)-coordinate system are used in the simple power in equation (6.4), the biaxial area moment of inertia \(I_{yz}\) can be positive, negative, or even zero.

The latter case always occurs when the cross-sectional area has symmetry about at least one of the axes:

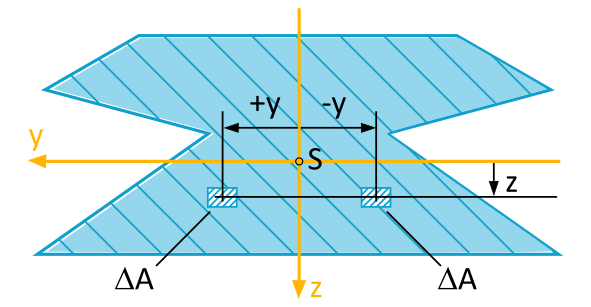
The illustration depicts a cross-sectional area symmetric with respect to the downward positive z-axis. At an equal distance from the z-axis, two infinitesimal surface elements are shown on the left and right, dimensioned with +y and -y. The vertical position of both elements is z.
Fig. 6.1.3: Biaxial Area Moment of Inertia in symmetrical cross-sectional areas

As shown in Figure 6.1.3, for example, in the case of symmetry about the \(z\)-axis, for every area element \(\Delta A\) with a positive distance \(y\), there is always an element with an equal negative distance.

Therefore, the integral \(I_{yz} = -\int\limits_{(A)} y \cdot z \ \mathrm{d}A\) over the entire area is zero in this case.

Note:

Why is the biaxial area moment of inertia defined as negative?

This is because it allows the equations for coordinate transformation for a rotation of the coordinate system to be structured in a comparable way as the equations for coordinate transformation of the stress or strain state.

The sign of the biaxial area moment of inertia is, by the way, a conventional definition and has no influence on the actual mechanical properties of the cross-section.