1.2.3 Definition des biaxialen Flächenträgheitsmomentes
Das biaxiale Flächenträgheitsmoment (auch: Deviationsmoment oder Zentrifugalmoment) ist eine geometrische Größe, die in der Technischen Mechanik Anwendung findet, wenn ein asymmetrischer Balkenquerschnitt einer geraden Biegung ausgesetzt ist oder eine asymmetrische Belastung (eine bestimmte Art der schiefen Biegung) auftritt.
In solchen Fällen ist das biaxiale Flächenträgheitsmoment wichtig, da es die Trägheit des Querschnitts gegenüber einer Biegebelastung berücksichtigt, die in zwei Richtungen wirkt, und nicht "nur" um die \(y\)- oder \(z\)-Achse.
(6.4)
Da die Abstände \(y\) und \(z\) des infinitesimalen Flächenelementes \(\mathrm{d}A\) zum Ursprung des \(y\),\(z\)-Koordinatensystems in der Gleichung (6.4) in einfacher Potenz eingesetzt werden, kann das biaxiale Flächenträgheitsmoment \(I_{yz}\) positiv, negativ oder auch Null sein.
Letzterer Fall tritt immer dann auf, wenn die Querschnittsfläche eine Symmetrie bezüglich mindestens einer der Achsen besitzt:
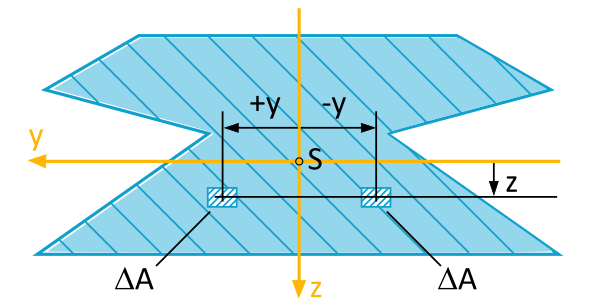
Wie in Abbildung 6.1.3 zu sehen ist, existiert beispielsweise bei Symmetrie bezüglich der \(z\)-Achse zu jedem Flächenelement \(\Delta A\) mit positivem Abstand \(y\) immer auch ein Element mit gleichem negativen Abstand.
Das Integral \(I_{yz} = -\int\limits_{(A)} y \cdot z \ \mathrm{d}A \) über die gesamte Fläche ist daher in diesem Fall Null.
Anmerkung:
Warum wird das biaxiale Flächenträgheitsmoment negativ definiert?
Dies hat den Hintergrund, dass dadurch die Gleichungen für die Koordinatentransformation für eine Drehung des Koordinatensystems vergleichbar aufgebaut sind wie die Gleichungen für die Koordinatentransformation des Spannungs- oder Verzerrungszustandes.
Das Vorzeichen des biaxialen Flächenträgheitsmomentes ist im Übrigen eine konventionelle Festlegung und hat keinen Einfluss auf die tatsächlichen mechanischen Eigenschaften des Querschnitts.