2. Calculation Methods for Arbitrary Shapes
In the following, we will explain the methods for calculating the moments of inertia \(I_y\), \(I_z\), and \(I_{yz}\) for areas of any shape using Cartesian coordinates and polar coordinates. There are a total of six different approaches available, of which the following four will be presented in more detail, each illustrated with an example. The choice of which approach to use depends on how we can construct the infinitesimal area element \(dA\), as it is contained in equations (6.2) - (6.4), and whether Cartesian coordinates or polar coordinates are employed.
2.1 Use of Cartesian Coordinates
2.1.1 Infinitesimal Area Element
We are working with a tiny area element \(dA\) with side lengths \(dy\) and \(dz\), as shown in Figure 6.2.1.

Since this area element is infinitesimal in both coordinate directions, we need a double integral to perform the calculation:
(6.5)
To apply this formula, it is necessary to determine the functional relationship \(z(y)\). If this is not possible, an alternative option is to use the integration limits \(z\) and \(y(z)\).
Example 6.1: Determining Area Moment of Inertia using the Calculation Method for Arbitrary Shapes Infinitesimal Area Element in Cartesian Coordinates
For the quarter-circle area depicted, the following area moments of inertia with respect to the illustrated \(y\), \(z\)-coordinate system are to be determined using the calculation method infinitesimal area element in Cartesian coordinates:

- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
Solution
To apply the required calculation method, it is necessary to determine the functional relationship \(z(y)\).
This can be found by examining the relationship between any value \(y\), its corresponding value \(z(y)\), and the radius of the (quarter) circle:

We recognize a right-angled triangle, and by using the Pythagorean theorem, we obtain the equation of the circle.
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.
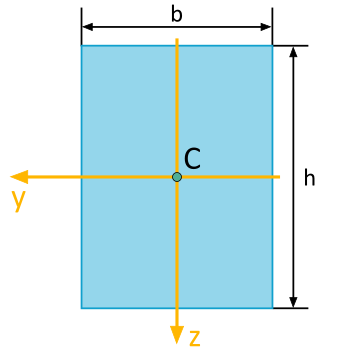
Determine the Area Moment of Inertia
For the rectangle area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
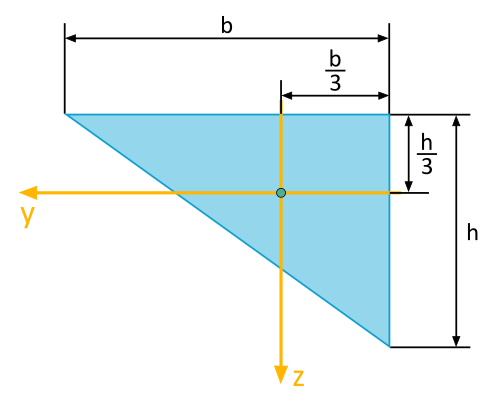
Determine the Area Moment of Inertia
For the triangle area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
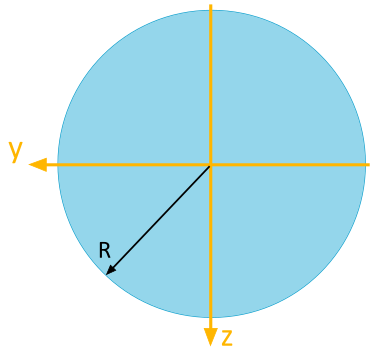
Determine the Area Moment of Inertia
For the circular area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)


