Mechanics of Materials

2.3 Mohr's Circle for Uniaxial Stress State

So, you're up for learning about Mohr's Circle? That's awesome! Don't worry, it's not as complicated as it looks.

2.3.1 The Equation of Mohr's Circle

In the previous section, we learned how to calculate the normal stress \(\sigma_{\xi}\) and the shear stress \(\tau_{\eta\xi}\) under an arbitrary cutting angle:

or

But who wants to juggle long formulas forever?

With this brilliant tool, you can easily visualize stresses graphically. But why is it called a stress circle and not a stress ellipse or stress rectangle? Let's derive the circle ourselves and see where it comes from. It's easy!

1. Rearranging the formulas:
   • Equation (1.4) for \(\cos(2\varphi)\):
     $$ \begin{align} \tag{1} \cos(2\varphi) &= \dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1 \end{align} $$
   • Equation (1.5) for \(\sin(2\varphi)\):
     $$ \begin{align} \tag{2} \sin(2\varphi) &= \mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x} \end{align} $$
2. Invoking Pythagoras:
   • Square both equations and add them.
     $$ \begin{align} \tag{3} \cos^2(2\varphi) + \sin^2(2\varphi) &= \Biggl(\dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1\Biggr)^2 + \Biggl(\mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x}\Biggr)^2 \end{align} $$
     Using the Pythagorean identity \(\sin^2(2\varphi)+\cos^2(2\varphi)=1\), we get:
     $$ \begin{align} \tag{4} 1 &= \Biggl(\dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1\Biggr)^2 + \Biggl(\mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x}\Biggr)^2 \end{align} $$
3. Some algebraic manipulation:
   • Expand the parentheses:
     $$ \begin{align} \tag{5} 1 &= \dfrac{4 \cdot \sigma^2_{\xi}}{\sigma^2_x} - \dfrac{4 \cdot \sigma_{\xi}}{\sigma_x} + 1 + \dfrac{4 \cdot \tau^2_{\xi_\eta}}{\sigma^2_x} \end{align} $$
   • Combine terms:
     $$ \begin{align} \tag{6} 1 &= \dfrac{4}{\sigma^2_x} \cdot \Biggl[\sigma^2_{\xi} - \sigma_{\xi} \cdot \sigma_x + \dfrac{\sigma^2_x}{4} + \tau^2_{\xi_\eta}\Biggr]\\[10pt] \tag{7} 1 &= \biggl(\dfrac{2}{\sigma_x}\biggr)^2 \cdot \Biggl[\sigma^2_{\xi} - \sigma_{\xi} \cdot \sigma_x + \biggl(\dfrac{\sigma_x}{2}\biggr)^2 + \tau^2_{\xi_\eta}\Biggr] \end{align} $$
     Now, let's play some algebraic switcheroo! Take that bracketed value we just freed and flip it like a pancake, sending it to the left side of the equation as its reciprocal. At the same time, let's smash the first three buddies in those square brackets together. You know, like combining like terms with the magical second term formula.
4. Tadaa! The circle equation:
   • Don't worry, you don't have to memorize it!
     $$ \begin{aligned} \biggl(\dfrac{\sigma_x}{2}\biggr)^2 = \biggl(\sigma_{\xi} - \dfrac{\sigma_x}{2}\biggr)^2 + \tau^2_{\xi_\eta} \end{aligned} $$

     (1.6)

It's simple! Look at the general equation of a circle:

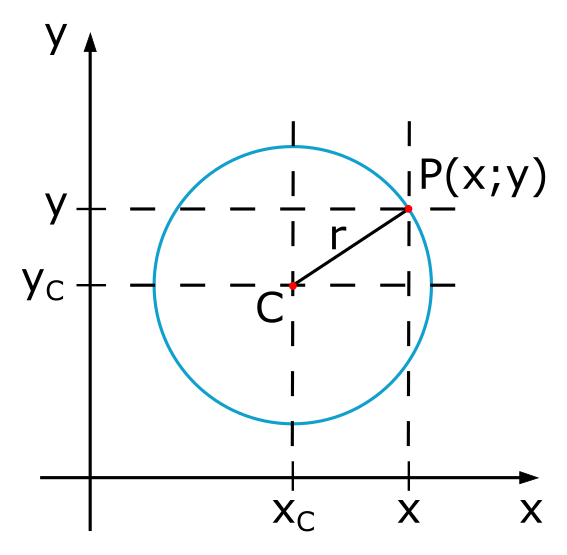
We have a circle with:

• Radius \(r\)
• Center \(x_C, y_C\)

• Our Equation (1.6) describes exactly such a circle!
• With radius \(\frac{\sigma_x}{2}\) and center \((\frac{\sigma_x}{2};0)\)

• In the circle equation, \(x\) and \(y\) are the coordinates of a point on the circle.
• In our equation, \(\sigma_{\xi}\) and \(\tau_{\xi\eta}\) are the "coordinates" of the stress states.

• Circle in the \(\sigma\), \(\tau\) plane: Sounds complicated, but it's actually easy.
• Center: \((\frac{\sigma_x}{2};0)\) - Some math involved, but nothing too bad.
• Radius: \(\frac{\sigma_x}{2}\) - Not so bad, right?
• Stress pairs \((\sigma_{\xi} ; \tau_{\xi\eta})\): Here things get a bit nerdy again.

A picture is worth a thousand words:

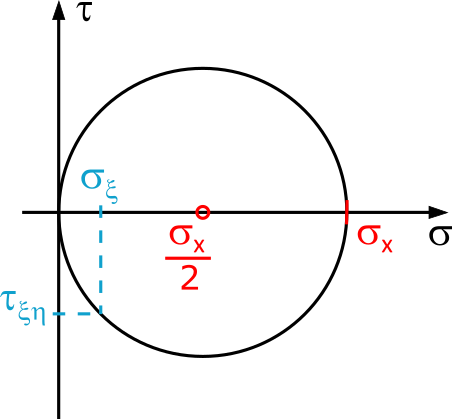
This circle is named after the German engineer and structural analyst Christian Otto Mohr (1835-1918) and is known as Mohr's Circle.

Read on to discover the full power of Mohr's Circle!

P.S.: Once you understand Mohr's Circle, you'll never forget it! So, give it a try, it's worth it!