Festigkeitslehre / Elastostatik

2.3 Mohrscher Spannungskreis für den einachsigen Spannungszustand

Du hast Bock auf den Mohrschen Spannungskreis? Coole Sache! Aber keine Panik, es ist gar nicht so kompliziert, wie es aussieht.

2.3.1 Die Kreisgleichung des Mohr'schen Spannungskreises

Im letzten Abschnitt haben wir gelernt, wie man die Normalspannung \(\sigma_{\xi}\) und die Schubspannung \(\tau_{\eta\xi}\) unter einem beliebigen Schnittwinkel berechnet:

oder

Aber hey, wer will schon ewig lange Formeln wälzen?

Mit diesem genialen Tool kannst du die Spannungen einfach grafisch darstellen. Doch warum heißt es Spannungskreis und nicht Spannungsellipse oder Spannungsrechteck? Entwickeln wir so einen Kreis am besten mal selber, dann wissen wir, wo er herkommt. So easy geht's:

1. Formeln umstellen:
   • Gleichung (1.4) nach \(\cos(2\varphi)\):
     $$ \begin{align} \tag{1} \cos(2\varphi) &= \dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1 \end{align} $$
   • Gleichung (1.5) nach \(\sin(2\varphi)\):
     $$ \begin{align} \tag{2} \sin(2\varphi) &= \mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x} \end{align} $$
2. Pythagoras zaubern:
   • Quadriere beide Gleichungen und addiere sie.
     $$ \begin{align} \tag{3} \cos^2(2\varphi) + \sin^2(2\varphi) &= \Biggl(\dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1\Biggr)^2 + \Biggl(\mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x}\Biggr)^2 \end{align} $$
     Es folgt mit \(\sin^2(2\varphi)+\cos^2(2\varphi)=1\):
     $$ \begin{align} \tag{4} 1 &= \Biggl(\dfrac{2 \cdot \sigma_{\xi}}{\sigma_x}-1\Biggr)^2 + \Biggl(\mp\dfrac{2 \cdot \tau_{\xi_\eta}}{\sigma_x}\Biggr)^2 \end{align} $$
3. Etwas hin- und her schieben:
   • Klammern auflösen:
     $$ \begin{align} \tag{5} 1 &= \dfrac{4 \cdot \sigma^2_{\xi}}{\sigma^2_x} - \dfrac{4 \cdot \sigma_{\xi}}{\sigma_x} + 1 + \dfrac{4 \cdot \tau^2_{\xi_\eta}}{\sigma^2_x} \end{align} $$
   • Terme zusammenfassen:
     $$ \begin{align} \tag{6} 1 &= \dfrac{4}{\sigma^2_x} \cdot \Biggl[\sigma^2_{\xi} - \sigma_{\xi} \cdot \sigma_x + \dfrac{\sigma^2_x}{4} + \tau^2_{\xi_\eta}\Biggr]\\[10pt] \tag{7} 1 &= \biggl(\dfrac{2}{\sigma_x}\biggr)^2 \cdot \Biggl[\sigma^2_{\xi} - \sigma_{\xi} \cdot \sigma_x + \biggl(\dfrac{\sigma_x}{2}\biggr)^2 + \tau^2_{\xi_\eta}\Biggr] \end{align} $$
     Bringe den ausgeklammerten Wert als Kehrwert auf die linke Seite der Gleichung. Fasse gleichzeitig die ersten drei Summanden in der eckigen Klammer zur 2. binomischen Formel zusammen.
4. Tadaa! Die Kreisgleichung:
   • Voila, fertig ist die magische Formel! Aber keine Sorge, du musst sie nicht auswendig lernen.
     $$ \begin{aligned} \biggl(\dfrac{\sigma_x}{2}\biggr)^2 = \biggl(\sigma_{\xi} - \dfrac{\sigma_x}{2}\biggr)^2 + \tau^2_{\xi_\eta} \end{aligned} $$

     (1.6)

Ganz einfach: Schau dir mal die allgemeine Kreisgleichung an:

Wir haben einen Kreis mit:

• Radius \(r\)
• Mittelpunkt \(x_M, y_M\)

• Unsere Gleichung 1.6 beschreibt genau so einen Kreis!
• Mit dem Radius \(\frac{\sigma_x}{2}\) und dem Mittelpunkt \((\frac{\sigma_x}{2};0)\)

• In der Kreisgleichung sind \(x\) und \(y\) die Koordinaten eines Punktes auf dem Kreis.
• In unserer Gleichung sind \(\sigma_{\xi}\) und \(\tau_{\xi\eta}\) die "Koordinaten" der Spannungszustände.

• Kreis in der \(\sigma\), \(\tau\) -Ebene: Klingt kompliziert, ist aber eigentlich ganz easy.
• Mittelpunkt: \((\frac{\sigma_x}{2};0)\) - Ja, okay, ein bisschen Mathe ist schon dabei.
• Radius: \(\frac{\sigma_x}{2}\) - Halb so wild, oder?
• Spannungspaare \((\sigma_{\xi} ; \tau_{\xi\eta})\): Okay, hier wird's wieder etwas nerdig.

Ein Bild sagt mehr als tausend Worte:

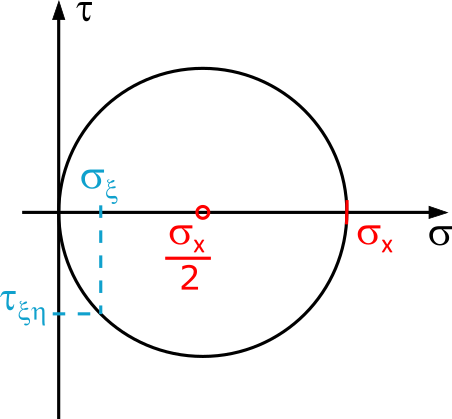
Dieser Kreis ist nach dem deutschen Ingenieur und Baustatiker Christan Otto Mohr (1835-1918) benannt und als Mohrscher Spannungskreis bekannt.

Dann lies weiter und entdecke die ganze Power des Mohrschen Spannungskreises!

P.S.: Wer den Mohrschen Spannungskreis einmal verstanden hat, kann ihn für immer! Also, streng dich an, es lohnt sich!