Step 4 | TechMechAcademy

Step 3: Determining the Shear Force $Q_\eta$ as a Function of the Angle $\varphi$

For which Angles $\varphi$ are the Normal Stress $\sigma_\xi$ and the Shear Stress $\tau_{\xi\eta}$ Maximum?

On this Page

Practice Exercises

Table of Contents

Step 4: Deriving the Formulas for Normal Stress $\sigma_\xi$ and Shear Stress $\tau_{\xi\eta}$ from Previous Results

Crack the stress code, math genius!

Ready for the next mission? This time we're hunting down the formulas for normal and shear stress at an arbitrary cutting angle $\varphi$.

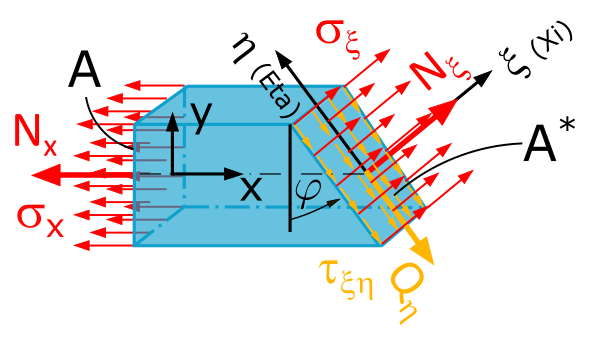
This figure shows a cross-section at an arbitrary angle Phi and the normal and shear stresses acting on it. — Fig. 1.2.11: Forces and stresses at the rotated $x$,$y$-coordinate system

Normal stress $\sigma_\xi$

Let's crack the code for $\sigma_\xi$ first:

$$ \begin{align} \tag{1} \sigma_\xi = \dfrac{N_\xi}{A^*} \end{align} $$

With some trigonometry magic and our previous results, we conjure up the formula:

$$ \begin{align} \tag{2} \sigma_\xi &= \dfrac{N_x \cdot \cos(\varphi)}{\dfrac{A}{\cos(\varphi)}}\\[10pt] \tag{3} \sigma_\xi &= \dfrac{N_x \cdot \cos(\varphi) \cdot \cos(\varphi)}{A}\\[10pt] \tag{4}\sigma_\xi &= \dfrac{N_x}{A} \cdot \cos^2(\varphi) \end{align} $$

We can simplify this equation further. Since $\sigma_x = \frac{N_x}{A}$, we have:

$$ \begin{align} \tag{5} \sigma_\xi = \sigma_x \cdot \cos^2(\varphi) \end{align} $$

Pretty elegant, huh? We already know $\sigma_x$ and $\varphi$ is simply the cutting angle. But wait, there's more! With another trigonometric formula, we can simplify the equation: With

$$ \begin{align} \tag{6} \cos^2(\varphi) = \dfrac{1}{2}\bigl(1+\cos(2\varphi)\bigr) \end{align} $$

we get:

$$ \begin{aligned} \sigma_\xi = \dfrac{\sigma_x}{2}\bigl(1+\cos(2\varphi)\bigr) \end{aligned} $$

(1.4)

See? Now we have the formula for $\sigma_\xi$ in all its glory!

Shear stress $\tau_{\xi\eta}$

Next up, let's tackle shear stress $\tau_{\xi\eta}$. The formula is similar, but we have to be careful:

$$ \begin{align} \tag{7} \tau_{\xi\eta} = \dfrac{Q_\eta}{A^*} \end{align} $$

Again, we use some trigonometry magic and our previous results to create the formula:

$$ \begin{align} \tag{8} \tau_{\xi\eta} &= \dfrac{N_x \cdot \sin(\varphi)}{\dfrac{A}{\cos(\varphi)}}\\[10pt] \tag{9} \tau_{\xi\eta} &= \dfrac{N_x \cdot \sin(\varphi) \cdot \cos(\varphi)}{A}\\[10pt] \tag{10} \tau_{\xi\eta} &= \dfrac{N_x}{A} \cdot \sin(\varphi) \cdot \cos(\varphi) \end{align} $$

We can simplify this equation further. Since $\sigma_x = \frac{N_x}{A}$, we have:

$$ \begin{align} \tag{11} \tau_{\xi\eta} = \sigma_x \cdot \sin(\varphi) \cdot \cos(\varphi) \end{align} $$

With another trigonometric formula, we can simplify the equation: With

$$ \begin{align} \tag{12} \sin(\varphi) \cdot \cos(\varphi) = \dfrac{1}{2}\bigl(\sin(2\varphi)\bigr) \end{align} $$

we get:

$$ \begin{align} \tag{13} \tau_{\xi\eta} = \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{align} $$

Attention! This formula is only valid for a coordinate system where shear stress is positive in the downward right direction.

Why? Let's recall the sign convention for shear stress. It depends on the coordinate system used.

We assumed a positive shear stress in the downward right direction. You can verify this again in the force triangle of Figure 1.2.10.

We need to adjust the sign in other coordinate systems.

Formula magic for rotated coordinate systems:

$x$,$y$-system

$$ \begin{aligned} \tau_{\xi\eta} = -\dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$

(1.5_xy)
$x$,$z$-system

$$ \begin{aligned} \tau_{\xi\eta} = \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$

(1.5_xz)

Mission accomplished! With these formulas, you can calculate normal and shear stress at any cutting angle.

By the way: These formulas are brilliant, but not infallible. Don't forget to keep an eye on the units!

P.S.: Thirsty for more math action? Take a closer look at the trigonometric relations. There are more exciting secrets to uncover!

Extra tip: These formulas are incredibly useful when you need to calculate stresses in components. For example, you can use them to determine whether a component can withstand a specific load.

Practice Exercise

Practice Exercise F-1.1.4

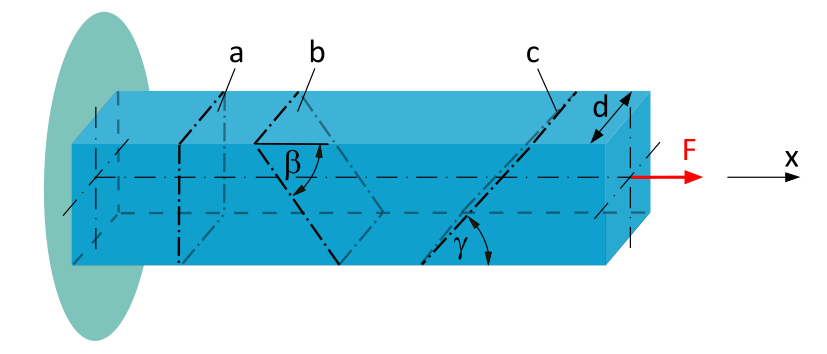
The illustration shows a beam with a square cross-section, fixed on the left side. In the drawing, three sectional planes a, b, and c are indicated. Sectional plane a is perpendicular to the beam axis. Sectional plane b runs from the upper left to the lower right, with the given angle Beta describing the smaller angle at the top. Sectional plane c runs from the lower left to the upper right, with the given angle Gamma describing the smaller angle at the bottom. The side length of the cross-section is denoted as d. A tensile force F acts at the right end of the beam at the center of the cross-section.

Normal and Shear Stress at an Arbitrary Section Angle

A clamped beam with a square cross-section (side length $d=20~\mathrm{mm}$) is subjected to a tensile force $F=10~\mathrm{kN}$ along the beam axis.

Determine the average normal stress and the average shear stress...

...acting in cross-sectional plane a.
...acting in cross-sectional plane b ($\beta = 50°$).
...acting in cross-sectional plane c ($\gamma = 40°$).

Mechanics of Materials

Stress State: Dive into the World of Forces and Stresses!

Step 4: Deriving the Formulas for Normal Stress \(\sigma_\xi\) and Shear Stress \(\tau_{\xi\eta}\) from Previous Results

Normal and Shear Stress at an Arbitrary Section Angle