Aufgabe M-D-1.6
Differentialrechnung: Differenzenquotienten und gemeinsame Tangenten von 2 Funktionen
Aufgabenstellung
Gegeben sind die Funktionen
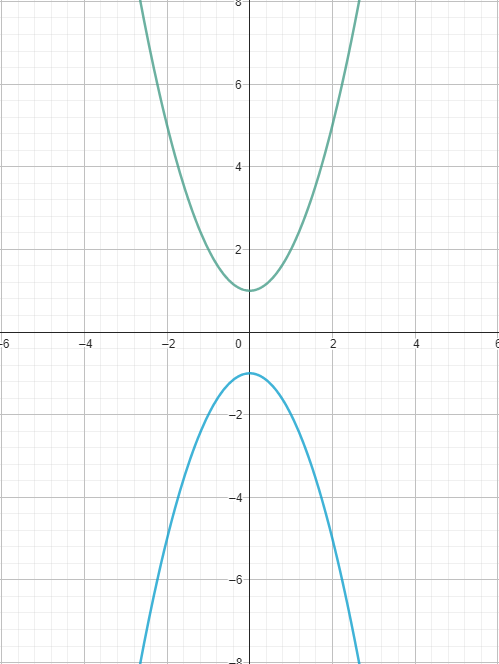
$$ f:x \mapsto f(x) = x^2+1,~D_f = \mathbb{R} $$
und
$$ g:x \mapsto g(x) = -x^2-1,~D_g = \mathbb{R} $$
- Bestimme die Ableitungen \(f^\prime\) und \(g^\prime\) als Grenzwert des Differenzenquotienten.
- Gebe die gemeinsamen Tangenten der Graphen von \(f(x)\) und \(g(x)\) an.
Kurzlösung
a. Bestimme die Ableitungen \(f^\prime\) und \(g^\prime\) als Grenzwert des Differenzenquotienten.
$$ \begin{aligned}
f^{\prime}(x_0) &= 2x_0 \\[7pt]
g^{\prime}(x_0) &= -2x_0
\end{aligned} $$
b. Gebe die gemeinsamen Tangenten der Graphen von \(f(x)\) und \(g(x)\) an.
$$ \begin{aligned}
t_1(x) &= 2x \\[7pt]
t_2(x) &= -2x
\end{aligned} $$
Ausführlicher Lösungsweg
a. Bestimme die Ableitungen \(f^\prime\) und \(g^\prime\) als Grenzwert des Differenzenquotienten.
Müssen wir die Ableitung einer Funktion als Grenzwert des Differenzenquotienten bestimmen, so benötigen wir die Formel für die Ableitung von \(f\) and der Stelle \(x_0\) (auch: Differentialquotient von \(f\) an der Stelle \(x_0\)):
$$ \begin{align}
\tag{1} f^{\prime}(x_0) &= \lim \limits_{h \to 0} \dfrac{f(x_0+h)-f(x_0)}{h}
\end{align} $$
Für alle \(x_0 \in \mathbb{R}\) und alle \(h \neq 0\) gilt
Weiterlesen mit TechMechAcademy+
Alles. Immer. Überall.
Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.
Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.




