1. Einführung
Im Bereich der Ingenieurmechanik ist das Verständnis des Verhaltens von Strukturen und Materialien von höchster Bedeutung. Ob du eine Brücke entwirfst, die enormen Belastungen standhalten muss, oder die Spannungsverteilung in einem mechanischen Bauteil analysierst: du wirst dich in der komplexen Landschaft der Mechanik wiederfinden. Im Herzen dieser Reise liegt das Konzept des Flächeträgheitsmomentes, ein grundlegendes und leistungsstarkes Werkzeug, das Ingenieure verwenden, um die Reaktion von Strukturen auf verschiedene Kräfte und Lasten vorherzusagen und zu steuern.
Genau wie das Flächenmoment erster Ordnung (der Schwerpunkt) den Massenschwerpunkt einer Form beschreibt, geht das Flächenträgheitsmoment tiefer in die Geometrie ein und charakterisiert ihren Widerstand gegen Biegung oder Verformung. Dieses Kapitel taucht in die Essenz dieses Konzepts ein, beleuchtet seine Anwendungen, mathematischen Grundlagen und praktischen Auswirkungen.
Wir werden erkunden, wie das Flächenträgheitsmoment eine entscheidende Rolle bei der Bestimmung von Durchbiegungen, Spannungen und Stabilität in Strukturen aller Größen spielt. Ob du ein Bauingenieur bist, der Wolkenkratzer entwirft, oder ein Maschinenbauingenieur, der ein Maschinenbauteil optimiert: das Verstehen der Feinheiten des Flächenträgheitsmomentes ist dein Ticket zum Erfolg in der Ingenieurwelt.
Bereite dich darauf vor, eine Reise durch die mathematischen Feinheiten, praktischen Beispiele und realen Anwendungen anzutreten, die es dir ermöglichen, die anspruchsvollsten ingenieurtechnischen Probleme selbstbewusst und präzise anzugehen. Willkommen in der Welt des Flächenträgheitsmoments, in der die formenden Kräfte der Ingenieurmechanik ans Licht gebracht werden.
1.1 Was ist ein Flächenträgheitsmoment?
Ein Flächenträgheitsmoment ist eine geometrische Größe, also sozusagen eine Form-Größe. Sie sagt uns, wie gut der Querschnitt einer Fläche sich gegen Veränderungen in einer bestimmten Richtung wehren kann. Dies hilft uns zu verstehen, wie stark dieser Querschnitt Biegung, Schub und Torsion bzw. Drehung widerstehen kann. Das ist besonders nützlich, wenn wir Spannungen und Verformungen in technischen Bauteilen wie Balken, Trägern und Platten berechnen wollen.
Das Flächenträgheitsmoment hängt von der Geometrie des Querschnitts und dessen Anordnung zur Belastung ab. Deutlich wird dies bei Betrachtung der Abbildung 6.1.1:
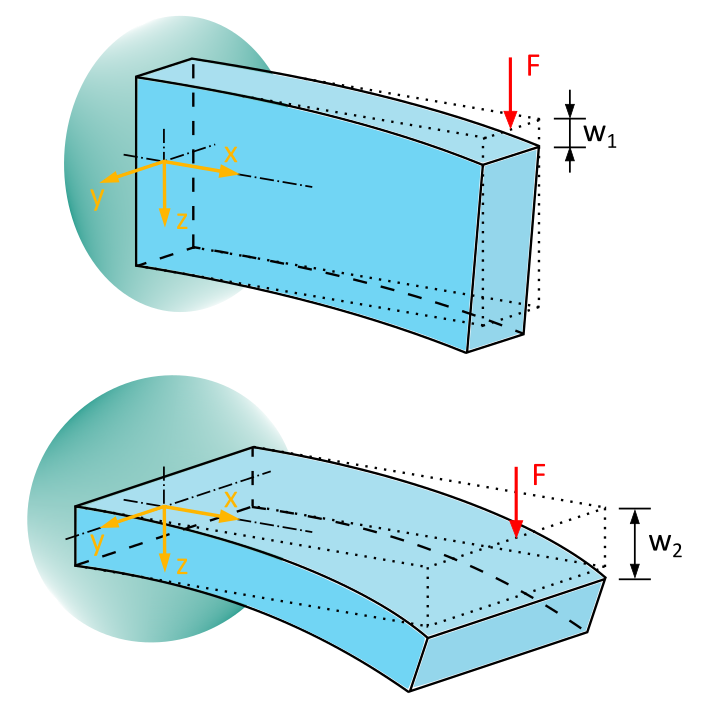
Wir sehen einen Balken mit einem rechteckigen Querschnitt. Dieser ist in der oberen Grafik hochkant und in der unteren Grafik im Querformat angeordnet. In beiden Fällen wird er von einer gleich großen Kraft F in \(z\)- Richtung belastet.
Durch die Kraft F wird der Balken verbogen. Es ist leicht vorstellbar, dass die Verformung w1 bei einer hochkanten Anordnung wesentlich geringer ausfällt als die Verformung w2 bei einer Anordnung im Querformat. Das heißt: Die Anordnung und Lage des Balkens sind bei gleicher Belastung für die Größe der Verbiegung verantwortlich.
Diese geometrische Größe, die eben diese Anordnung und Lage eines Querschnitts berücksichtigt, bezeichnet man als Flächenträgheitsmoment. Es beschreibt den Widerstand eines Balkenquerschnitts, also einer Fläche, gegen eine Belastung und somit gegen Verformungen.
Das Material des Bauteils hat keinen Einfluss auf das Flächenträgheitsmoment. Natürlich macht es für die Verformungen w1 und w2 einen Unterschied, ob das Material des Bauteils mehr oder weniger elastisch ist. Diese Eigenschaft muss also bei der Berechnung dieser Verformungen einfliessen, nicht aber bei der Bestimmung des Flächenträgheitsmoments.
Je größer das Flächenträgheitsmoment eines Querschnitts ist, desto steifer ist er und desto geringer sind die Verformungen bei einer bestimmten Belastung. Daher ist das Flächenträgheitsmoment ein wichtiger Parameter bei der Gestaltung und Berechnung von Bauteilen in der Maschinenbau-, Bau- und Luftfahrtindustrie.