Aufgabensammlung Festigkeitslehre / Elastostatik

Auf dieser Seite

Spannungszustand

Einachsiger Spannungszustand

Aufgabe F-1.1.1

Die Abbildung zeigt einen runden, sich verjüngenden Stab, der entlang seiner Symmetrieachse mit einer Druckkraft F, dargestellt durch zwei rote Pfeile, die auf die Kreisflächen am Stabanfang und -ende zeigen.

Konischer Stab und Druckkraft

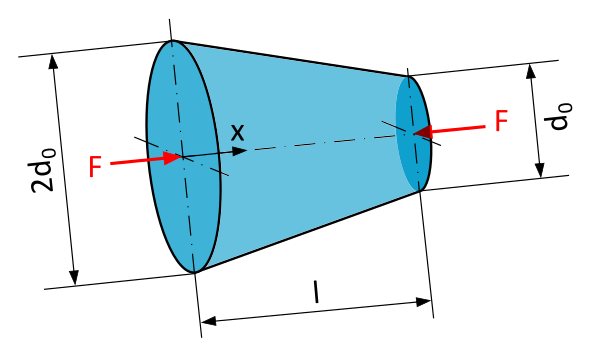
Ein konischer Stab mit kreisförmigem Querschnitt und der Länge $l=250~\mathrm{mm}$ wird wie in Abbildung 1 dargestellt durch eine Druckkraft $F=10~\mathrm{kN}$ in der Stabachse belastet. Der Durchmesser bei $x=0$ sei mit $2d_0=150~\mathrm{mm}$ doppelt so groß wie der Durchmesser bei $x=l$ mit $d_0=75~\mathrm{mm}$.

Wie lautet die Formel zur Berechnung der Normalspannung $\sigma$ an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabachse?
Wie groß ist die Normalspannung $\sigma$ an der Stelle $x=200~\mathrm{mm}$ in einem Schnitt senkrecht zur Stabachse?

Aufgabe F-1.1.2

Die Abbildung zeigt einen Kreiskegel, dessen Grundfläche oben und dessen Spitze unten angeordnet sind. Die Laufkoordinate x läuft von der Spitze des Kreiskegels nach oben. Die Erdbeschleunigung g ist mit einem Pfeil nach unten eingezeichnet.

Hängender Kreiskegel

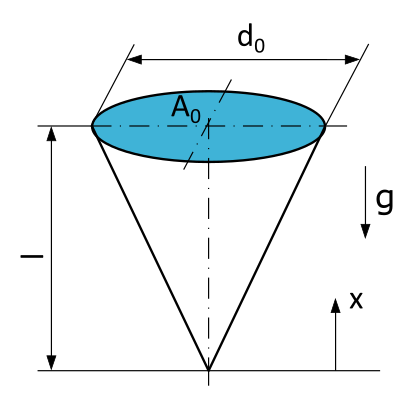
An einer Dachrinne hängt ein Eiszapfen. Der Zapfen besitzt die Form eines Kreiskegels mit der Länge $l=10~\mathrm{cm}$, der am Aufhängepunkt einen Durchmesser $d_0=5~\mathrm{cm}$ und eine Querschnittsfläche $A_0$ hat. Das Eis hat eine Dichte von $\varrho = 0,91~\mathrm{g/cm^3}$.

Wie lautet die Formel zur Berechnung der Normalkraft $N$ an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
Wie lautet die Formel zur Berechnung der Normalspannung $\sigma$ an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
Wie groß ist die Normalspannung $\sigma$ an der Stelle $x=70~\mathrm{mm}$ in einem Schnitt senkrecht zur Kegelachse?

Aufgabe F-1.1.3

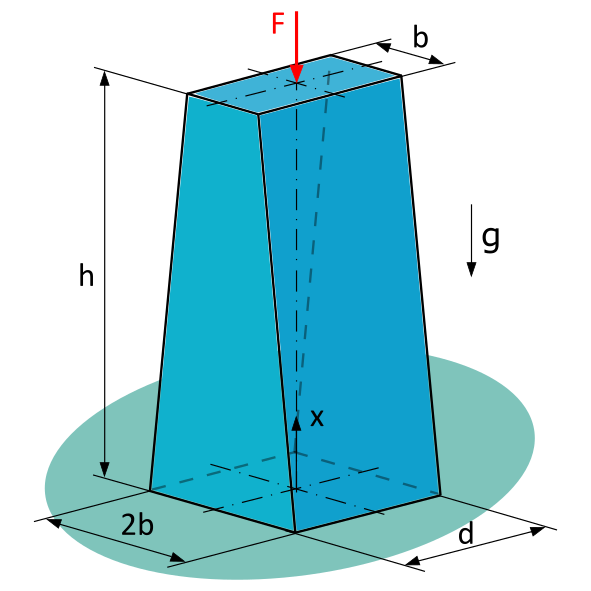
Der Stab steht auf einem angedeuteten Boden. Seine untere Grundfläche ist 2b x d, seine obere Grundfläche b x d. Seine Höhe ist mit h bemaßt. Von oben wird er von einer Kraft F, dargestellt durch einen nach unten gerichteten Pfeil, in seiner Symmetrieachse belastet. Die Laufkoordinate x läuft von unten nach oben. Die Erdbeschleunigung g ist mit einem Pfeil nach unten eingezeichnet.

Belasteter homogener Stab mit konstanter Dicke und linear veränderlicher Breite

Ein homogener Stab mit konstanter Dicke $d=20~\mathrm{mm}$ und linear veränderlicher Breite wird durch eine Druckkraft $F=1~\mathrm{kN}$ belastet.

Geg.: $b=15~\mathrm{mm}$, $h=80~\mathrm{mm}$, $\varrho = 7,85~\mathrm{g/cm^3}$

Wie lautet die Formel zur Berechnung der Querschnittsfläche $A(x)$ an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabachse?
Wie lautet die Formel zur Berechnung der Normalkraft $N(x)$ an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabachse?
Wie groß ist die Normalspannung $\sigma$ an der Stelle $x=30~\mathrm{mm}$ in einem Schnitt senkrecht zur Stabachse?

Aufgabe F-1.1.4

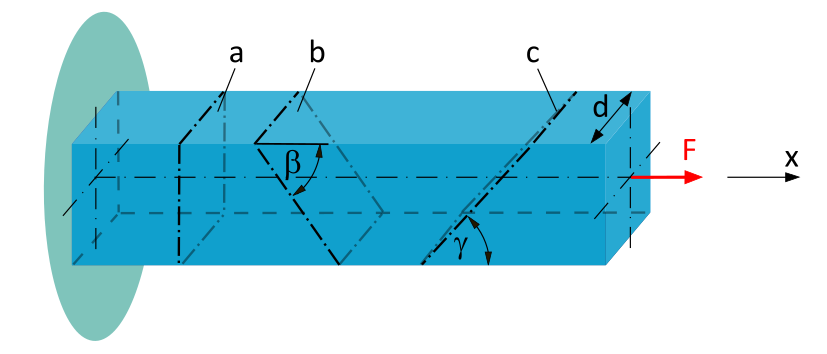
Die Abbildung zeigt einen linksseitig eingespannten Balken mit quadratischem Querschnitt. In der Zeichung sind drei Schnittebenen a, b und c angedeutet. Die Schnittebene a ist senkrecht zur Balkenachse. Die Schnittebene b verläuft von links oben nach rechts unten, der gegebene Winkel Beta beschreibt den kleineren Winkel oben. Die Schnittebene c verläuft von links unten nach rechts oben, der gegebene Winkel Gamma beschreibt den kleineren Winkel unten. Die Seitenlänge des Querschnittes ist die Länge d. Am rechten Balkenende wirkt eine Zugkraft F im Schwerpunkt des Querschnitts.

Normal- und Schubspannung unter beliebigem Schnittwinkel

Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge $d=20~\mathrm{mm}$) wird durch eine Zugkraft $F=10~\mathrm{kN}$ in der Balkenachse belastet.

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die

in der Schnittebene a wirken.
in der Schnittebene b ($\beta = 50°$) wirken.
in der Schnittebene c ($\gamma = 40°$) wirken.

Ebener Spannungszustand

Aufgabe F-1.2.1-xy

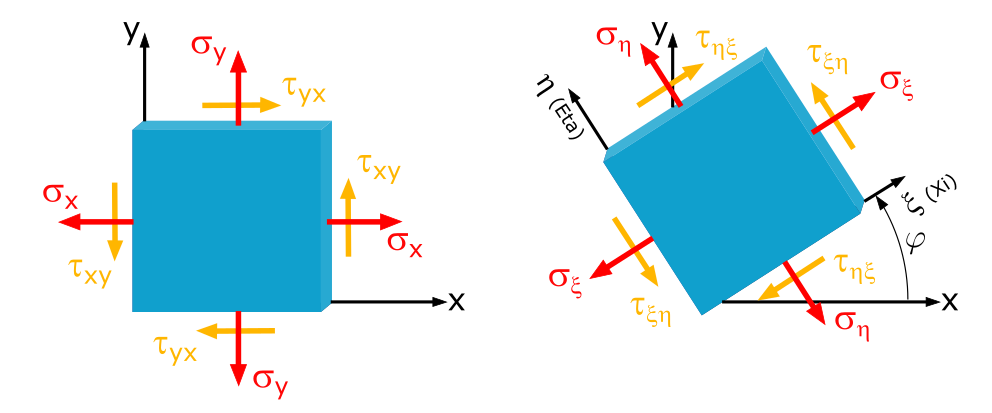
Diese Abbildung zeigt ein quadratisches Blech in zwei Positionen. Einmal liegt es mit zwei Seiten in einem x,y-Koordinatensystem mit Ursprung in der linken unteren Ecke des Bleches. In der zweiten Position wird es um einen Winkel Phi zur x-Achse gekippt. Die x-Achse ist nach rechts positiv, die y-Achse nach oben positiv. Normal- und Schubspannungen sind für jede Seite des Bleches jeweils positiv mit Pfeilen dargestellt.

Koordinatentransformation x,y-Koordinatensystem

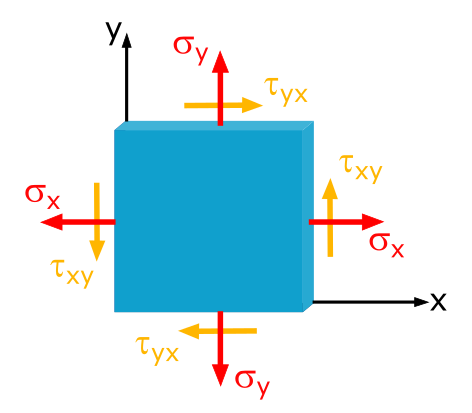
In einem Blech seien die Spannungen $\sigma_x = -250\mathrm{~MPa}$, $\sigma_y = 80\mathrm{~MPa}$ und $\tau_{xy} = 50\mathrm{~MPa}$ gegeben.

Welche Normal- und Schubspannungen treten unter einem Schnittwinkel von $\varphi=30°$ auf?

Aufgabe F-1.2.1-xz

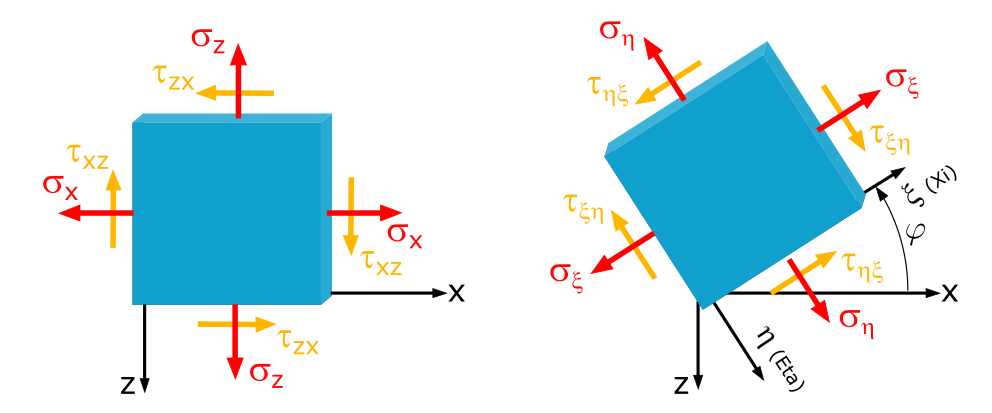
Diese Abbildung zeigt ein quadratisches Blech in zwei Positionen. Einmal liegt es mit zwei Seiten in einem x,z-Koordinatensystem mit Ursprung in der linken unteren Ecke des Bleches. In der zweiten Position wird es um einen Winkel Phi zur x-Achse gekippt. Die x-Achse ist nach rechts positiv, die z-Achse nach unten positiv. Normal- und Schubspannungen sind für jede Seite des Bleches jeweils positiv mit Pfeilen dargestellt.

Koordinatentransformation x,z-Koordinatensystem

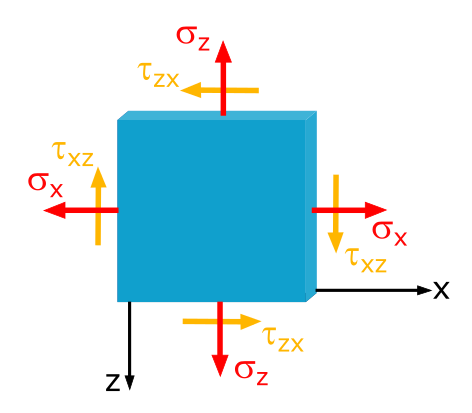
In einem Blech seien die Spannungen $\sigma_x = -250\mathrm{~MPa}$, $\sigma_z = 80\mathrm{~MPa}$ und $\tau_{xz} = 50\mathrm{~MPa}$ gegeben.

Welche Normal- und Schubspannungen treten unter einem Schnittwinkel von $\varphi=30°$ auf?

Aufgabe F-1.2.2-xy

Diese Abbildung zeigt ein quadratisches Blech. Es liegt mit zwei Seiten in einem x,y-Koordinatensystem mit Ursprung in der linken unteren Ecke des Bleches. Die x-Achse ist nach rechts positiv, die y-Achse nach oben positiv. Normal- und Schubspannungen sind für jede Seite des Bleches jeweils positiv mit Pfeilen dargestellt.

Größe und Richtung der Hauptspannungen bestimmen im x,y-Koordinatensystem

In einem Blech seien die Spannungen $\sigma_x = 20\mathrm{~MPa}$, $\sigma_y = 30\mathrm{~MPa}$ und $\tau_{xy} = 10\mathrm{~MPa}$ gegeben.

Bestimme die Größe und Richtung der Hauptspannungen.

Aufgabe F-1.2.2-xz

Diese Abbildung zeigt ein quadratisches Blech. Es liegt mit zwei Seiten in einem x,z-Koordinatensystem mit Ursprung in der linken unteren Ecke des Bleches. Die x-Achse ist nach rechts positiv, die z-Achse nach unten positiv. Normal- und Schubspannungen sind für jede Seite des Bleches jeweils positiv mit Pfeilen dargestellt.

Größe und Richtung der Hauptspannungen bestimmen im x,z-Koordinatensystem

In einem Blech seien die Spannungen $\sigma_x = 20\mathrm{~MPa}$, $\sigma_z = 30\mathrm{~MPa}$ und $\tau_{xz} = 10\mathrm{~MPa}$ gegeben.

Bestimme die Größe und Richtung der Hauptspannungen.

Flächenträgheitsmoment

Flächenträgheitsmoment: Berechnung beliebig geformter Flächen durch Integration

Aufgabe F-6.1.1

Viertelkreisfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Radius: R, Zentrum des Vollkreises: y,z, y nach links positiv, z nach unten positiv.

Flächenträgheitsmoment bestimmen

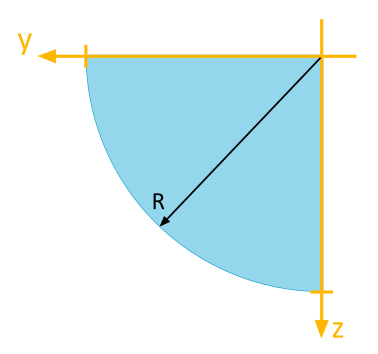
Für den abgebildeten Viertelkreis sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Aufgabe F-6.1.2

Rechteckfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Breite: b, Höhe h, Koordinatensystem y,z mit Zentrum im Schwerpunkt (b/2;h/2), y nach links positiv, z nach unten positiv.

Flächenträgheitsmoment bestimmen

Für das abgebildete Rechteck sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Aufgabe F-6.1.3

Dreieckfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Rechtwinkliges Dreieck, Rechter Winkel oben rechts. Breite: b, Höhe h, Koordinatensystem y,z mit Zentrum im Schwerpunkt (b/3 von rechter Seite;h/3 von oben), y nach links positiv, z nach unten positiv.

Flächenträgheitsmoment bestimmen

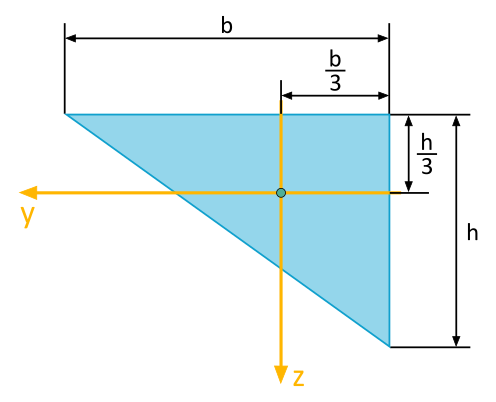
Für das abgebildete Dreieck sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Aufgabe F-6.1.4

Kreisfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Radius: R, Zentrum: y,z, y nach links positiv, z nach unten positiv.

Flächenträgheitsmoment bestimmen

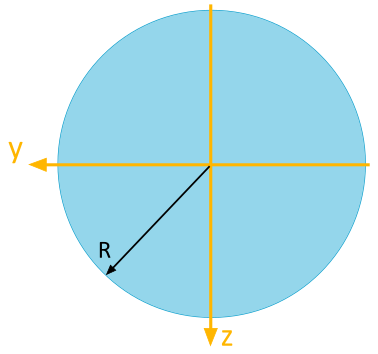
Für die abgebildete Kreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Flächenträgheitsmoment: Parallelverschiebung der Koordinatenachsen - Der Satz von Steiner

Übungsaufgabe F-6.2.1

Die Abbildung zeigt eine rechteckige Querschnittsfläche der Breite b und Höhe h. Ein gelbes y,z-Koordinatensystem liegt mit seinem Ursprung im Schwerpunkt des Rechtecks. Ein grünes y mit Überstrich,z mit Überstrich-Koordinatensystem liegt mit seinem Ursprung in der linken oberen Ecke des Rechtecks. Die y-Achsen sind nach links postiv, die z-Achsen nach unten positiv.

Bestimme Flächenträgheitsmomente für ein Koordinatensystem parallel zum Schwerachsensystem

Für das abgebildete Rechteck sind folgende Flächenträgheitsmomente bezüglich des dargestellten $\overline{y}$, $\overline{z}$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Gegeben sind die Flächenträgheitsmomente bezüglich der Schwerachsen:

$$ \begin{align} I_y &= \dfrac{b \cdot h^3}{12} \\[7pt] I_z &= \dfrac{b^3 \cdot h}{12} \\[7pt] I_{yz} &= 0 \end{align} $$

Übungsaufgabe F-6.2.2

Die Abbildung zeigt eine rechteckige Querchnittsfläche mit der Breite b und der Höhe h. Ein gelbes y,z-Koordinatensystem hat seinen Ursprung im Schwerpunkt der Fläche. Eine grüne y mit Überstrich Index 1-Achse befindet sich im Abstand a Index 1 parallel über der gelben y-Achse. Eine rote y mit Überstrich Index 2-Achse befindet sich im Abstand a Index 2 parallel unter der gelben y-Achse. Die y-Achsen sind nach links positiv, die z-Achse nach unten positiv.

Bestimme Flächenträgheitsmomente für ein Koordinatensystem parallel zum Schwerachsensystem

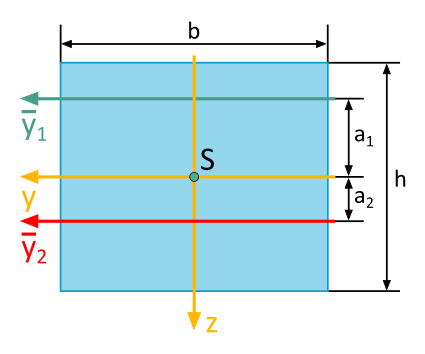
Der dargestellte Rechteckquerschnitt hat eine Fläche von $A=72~\mathrm{cm}^2$.

Das axiale Flächenträgheitsmoment bezogen auf die $\overline{y}_1$-Achse ($a_1 = 5~\mathrm{cm}$) ist bekannt und beträgt $I_{\overline{y}_1}=2664~\mathrm{cm}^4$.

Berechne das axiale Flächenträgheitsmoment $I_{\overline{y}_2}$ bezogen auf die $\overline{y}_2$-Achse ($a_2 = 2~\mathrm{cm}$).