Exercise F-1.1.3 TechMech 2 Mechanics of Materials

Practice Exercise F-1.1.3

Uniaxial Stress State: Loaded Homogeneous Bar with Constant Thickness and Linearly Varying Width

Problem Statement

A homogeneous bar with constant thickness $d=20~\mathrm{mm}$ and linearly varying width is subjected to a compressive force $F=1~\mathrm{kN}$.

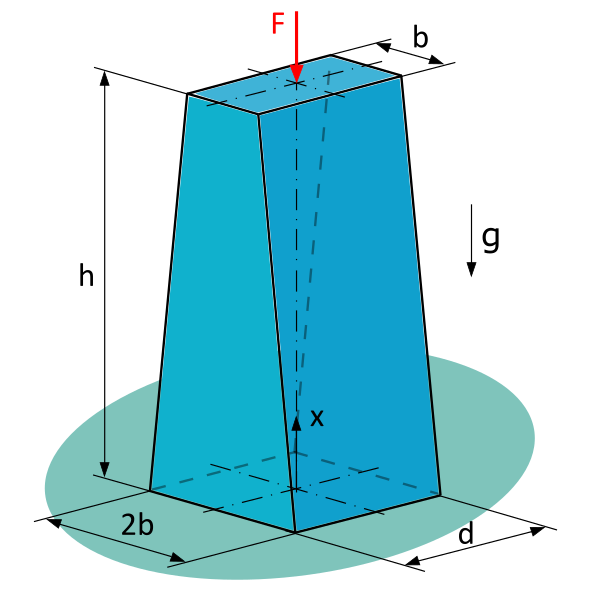
The rod stands on an indicated ground. Its lower base is 2b x d, its upper base is b x d. Its height is dimensioned as h. From the top, it is subjected to a force F, represented by a downward arrow, along its axis of symmetry. The running coordinate x extends from the bottom to the top. The gravitational acceleration g is indicated with an arrow pointing downward. — Fig. 1: Homogeneous bar with constant thickness and linearly varying width

Given: $b=15~\mathrm{mm}$, $h=80~\mathrm{mm}$, $\varrho = 7,85~\mathrm{g/cm^3}$

What is the formula for calculating the cross-sectional area $A(x)$ at any location x in a section perpendicular to the axis of the rod?
What is the formula for calculating the normal force $N(x)$ at any location x in a section perpendicular to the axis of the rod?
What is the magnitude of the normal stress $\sigma$ at the location $x=30~\mathrm{mm}$ in a section perpendicular to the axis of the rod?

Short Solution

What is the formula for calculating the cross-sectional area $A(x)$ at any location x in a section perpendicular to the axis of the rod?

$$ A(x) =b\cdot d \cdot \Bigl(2-\dfrac{x}{h}\Bigr) $$

What is the formula for calculating the normal force $N(x)$ at any location x in a section perpendicular to the axis of the rod?

$$ N(x) = \dfrac{1}{2} \varrho \cdot g \cdot b \cdot d \Bigl[x\Bigl(4 - \dfrac{x}{h}\Bigr) - 3h\Bigr] - F $$

What is the magnitude of the normal stress $\sigma$ at the location $x=30~\mathrm{mm}$ in a section perpendicular to the axis of the rod?

$$ \sigma(x=30~\mathrm{mm}) = -2,054 ~\frac{\mathrm{N}}{\mathrm{mm^2}} $$

Comprehensive Solution

Preliminary Considerations

So, you want to crack the stress state in the rod? Cool stuff! But no worries, it's a piece of cake.

First things first, chill out! The rod stands firm, not toppling over anytime soon. The compressive force is pushing down, including the weight force of the rod. But the support reactions hold their ground. That creates a uniaxial stress state – all easy, right?

Ultimately, in task c), you're on the lookout for the normal stress. For that, you need this formula:

$$ \begin{aligned} \sigma_x = \dfrac{N_x}{A} \end{aligned} $$

(1.3)

Okay, okay, looks complicated, but it's not that bad.

$N_x$ is the normal force in the cut. It depends on the weight force of the cut-off section of the rod. And thus, on the position $x$ in the rod: The higher you cut, the less rod mass presses downward, the smaller $N_x$.

$A$ is the cross-sectional area of the rod at point $x$. The higher you cut, the smaller the area, the smaller $A$.

You see, both $N_x$ and $A$ change with $x$. That's why you have to use formula 1.3b to calculate stress at every point $x$.

$$ \begin{aligned} \sigma(x) = \dfrac{N(x)}{A(x)} \end{aligned} $$

(1.3b)

But no panic! With a bit of math and patience, you've got this covered.

Tip: Imagine slicing the rod into many thin slices. Calculate the stress for each slice. That way, you get a feel for how stress is distributed in the rod.

Good luck! And if you're ever stuck, just peek into the complete solution below.

P.S.: Don't forget that the rod is made of a specific material. The material influences the stress. So, you still need to consider the material properties.

P.P.S.: Oh, and the units! Be careful to use the right units. Otherwise, the result won't be right in the end.

What is the formula for calculating the cross-sectional area $A(x)$ at any location x in a section perpendicular to the axis of the rod?

According to the problem statement, the rod has a constant thickness $d$ and a linearly varying width $B(x)$:

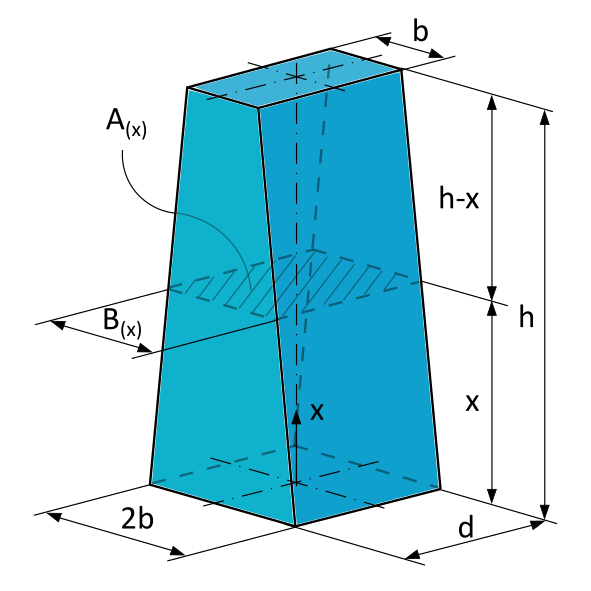
This illustration shows that the cross-sectional area of the rod changes with the position x. — Fig. 2: Cross-sectional area of the rod

The cross-sectional area is rectangular at each position $x$. Therefore, the formula is:

$$ \begin{align} \tag{1} A(x)=B(x) \cdot d \end{align} $$

We need to express the factor $B(x)$ as a function of $x$, while the factor $d$ is not dependent on $x$ and remains constant.

Due to the symmetry of the width view and the constant thickness $d$, we can simplify our considerations by only focusing on the range from the centerline to the outer edge.

Continue with TechMechAcademy+

Everything. Always. Everywhere.

With TechMechAcademy+ full access to all content.

For Beginners: TechMechAcademy+. Full access to all content for one day.

Overview of the benefits:

Most cost-effective offer.
Ideal if you need access to already identified content for a short period.
Unlimited access to all existing and newly created content throughout the entire premium membership.
Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.

€3.99

TechMechAcademy+. Full access to all content for one week.

Overview of the benefits:

Cost-effective offer.
Ideal for short-term exam preparation with the content of TechMechAcademy.
Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.

€9.99

Bestseller: TechMechAcademy+. Full access to all content for one month.

Overview of the benefits:

Benefit from the bestseller.
Ideal for effective exam preparation with the content of TechMechAcademy.
Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.

€14.99

TechMechAcademy+. Full access to all content for three months.

Overview of the benefits:

Cost-effective due to extended duration.
Ideal for working alongside the semester with the content of TechMechAcademy.
Unrestricted admission to all content, both pre-existing and recently generated, within the scope of the premium membership.
Guaranteed premium membership for three months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the third month from the start date. No cancellation necessary.

€29.99

TechMechAcademy+. Full access to all content for six months.

Overview of the benefits:

Cost-effective due to extended duration.
Ideal for semester preparation, concurrent semester work, and/or post-semester work with the content of TechMechAcademy.
Unrestricted entry to a comprehensive collection of both existing and freshly generated content as part of the premium membership.
Guaranteed premium membership for six months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the sixth month from the start date. No cancellation necessary.

€49.99

Become a TechMechAcademy+ Premium Member!

Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.