Aufgabe F-1.1.2
Einachsiger Spannungszustand: Hängender Kreiskegel
Aufgabenstellung
An einer Dachrinne hängt ein Eiszapfen. Der Zapfen besitzt die Form eines Kreiskegels mit der Länge \(l=10~\mathrm{cm}\), der am Aufhängepunkt einen Durchmesser \(d_0=5~\mathrm{cm}\) und eine Querschnittsfläche \(A_0\) hat. Das Eis hat eine Dichte von \(\varrho = 0,91~\mathrm{g/cm^3}\).
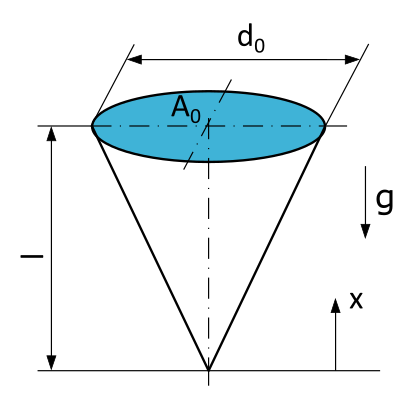
- Wie lautet die Formel zur Berechnung der Normalkraft \(N\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=70~\mathrm{mm}\) in einem Schnitt senkrecht zur Kegelachse?
Kurzlösung
- Wie lautet die Formel zur Berechnung der Normalkraft \(N\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie lautet die Formel zur Berechnung der Normalkraft \(N\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
Wenn man möchte, kann man noch \(r_0^2 \cdot \pi=A_0\) zusammenfassen und hat dann als finales Ergebnis:
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=70~\mathrm{mm}\) in einem Schnitt senkrecht zur Kegelachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=70~\mathrm{mm}\) in einem Schnitt senkrecht zur Kegelachse?
Ausführlicher Lösungsweg
Vorüberlegungen
Du willst den Spannungszustand im Kreiskegel knacken? Coole Sache! Aber keine Sorge, es ist gar nicht so schwer, wie es aussieht.
Zuerst mal: Entspann dich! Der Kegel steht hängt stabil da, er fällt nicht einfach herunter. Die Gewichtskraft zieht zwar nach unten, aber die Lagerreaktion, also die Verbindung Dachrinne-Eiszapfen, hält dagegen. So entsteht ein einachsiger Spannungszustand – alles easy.
Du suchst jetzt die Normalspannung in einem Schnitt senkrecht zur Stabachse. Dazu brauchst du die Formel:
(1.3)
Okay, okay, sieht kompliziert aus, aber ist halb so wild.
\(N_x\) ist die Normalkraft, die im Schnitt wirkt. Sie hängt von der Gewichtskraft des (ab-)geschnittenen Kegels ab. Und damit von der Position x im Kegel: Je weiter oben du schneidest, desto mehr Kegelmasse zieht nach unten, desto größer ist \(N_x\).
\(A\) ist die Querschnittsfläche des Kegels an der Stelle \(x\). Je weiter oben du schneidest, desto größer wird der Kreis, desto größer ist \(A\).
Du siehst, sowohl \(N_x\) als auch \(A\) ändern sich mit \(x\). Deswegen musst du die Formel 1.3b verwenden, um die Spannung an jeder Stelle \(x\) auszurechnen.
(1.3b)
Aber keine Panik! Mit ein bisschen Mathe und Geduld schaffst du das locker.
Tipp: Stell dir vor, du zerschneidest den Kegel in ganz viele dünne Scheiben. Für jede Scheibe berechnest du dann die Spannung. So bekommst du ein Gefühl dafür, wie sich die Spannung im Kegel verteilt.
Viel Erfolg! Und wenn du mal nicht weiterweißt, schaue einfach unten in die Komplettlösung.
P.S.: Vergiss nicht, dass der Kegel aus einem bestimmten Material besteht. Das Material hat Einfluss auf die Spannung. Du musst also noch die Materialeigenschaften berücksichtigen.
P.P.S.: Ach ja, und die Einheiten! Pass auf, dass du die richtigen Einheiten verwendest. Sonst stimmt am Ende das Ergebnis nicht.
- Wie lautet die Formel zur Berechnung der Normalkraft \(N\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
Schritt 1: Normalkraft \(N(x)\) anhand der Gleichgewichtsbedingungen bestimmen
Um die Normalkraft zu berechnen, schneiden wird den Stab an einem beliebigen Punkt \(x\) und tragen die äußere Kraft \(F_G\) und die innere Normalkraft \(N\) an.
Zur Erinnerung: Am positiven, linken Schnittufer tragen wir \(N\) in positiver (in Richtung der positiven x-Achse) Richtung an, am negativen, rechten Schnittufer hingegen in negativer (gegen die Richtung der positiven x-Achse) Richtung.
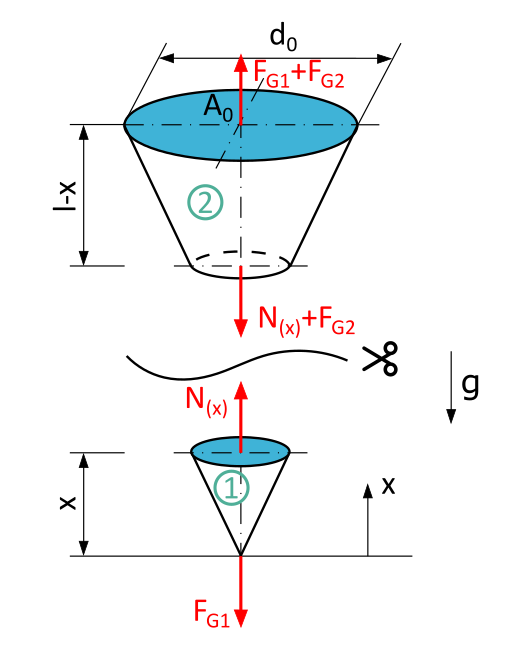
Bei dieser Aufgabe müssen wir beachten, dass die Gewichtskraft des "ab-"geschnittenen Kreiskegels von \(x\) abhängt: Je größer der geschnittene Kreiskegel, desto größer die Gewichtskraft dieses Kreiskegels (hier: \(F_{G1})\).
Zur Lösung dieser Aufgabe ist es eigentlich nicht erforderlich, auch den verbleibenden Kegelstumpf des Schnittes freizuschneiden. Aber der Vollständigkeit halber: Am rechten Schnittufer des Kegelstumpfes wirken zum einen die Reaktionsnormalkraft des Schnittes (hier heißt sie ebenfalls: \(N(x)\)) und zum anderen die Gewichtskraft des verbleibenden Kegelstumpfes (hier: \(F_{G2})\).
Dem entgegen wirkt die Lagerreaktion der Dachrinne, die der Gewichtskraft des gesamten Kreiskegels vor dem Schnitt entsprechen muss, da nur diese als äußere Belastung auftritt und sich der Eiszapfen in Ruhe befinden muss.
Die Vorteile im Überblick:
- Kostengünstigstes Angebot.
- Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
- Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
- Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.
3,99 €
Die Vorteile im Überblick:
- Kostengünstiges Angebot.
- Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unbeschränkter Zugang zu sämtlichen bestehenden und frisch erstellten Inhalten im Rahmen der gesamten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.
9,99 €
Die Vorteile im Überblick:
- Profitiere vom Bestseller.
- Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unlimitierter Zugriff auf alle bereits vorhandenen und neu geschaffenen Inhalte während der gesamten Dauer der Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.
14,99 €
Die Vorteile im Überblick:
- Kostengünstig durch lange Laufzeit.
- Ideal für semesterbegleitendes Arbeiten mit den Inhalten von TechMechAcademy.
- Freier Zugang zu sämtlichen bestehenden und neu erstellten Inhalten innerhalb der gesamten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von drei Monaten gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des dritten Monats ab dem Startdatum. Keine Kündigung notwendig.
29,99 €
Die Vorteile im Überblick:
- Kostengünstig durch lange Laufzeit.
- Ideal für semestervorbereitendes, semesterbegleitendes und/oder semesternachbereitendes Arbeiten mit den Inhalten von TechMechAcademy.
- Unbegrenzter Zugriff auf alle vorhandenen und neu geschaffenen Inhalte im Verlauf der kompletten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von sechs Monaten gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des sechsten Monats ab dem Startdatum. Keine Kündigung notwendig.
49,99 €
Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.




