Practice Exercise F-1.1.4
Uniaxial Stress State: Normal and Shear Stress at an Arbitrary Section Angle
Problem Statement
A clamped beam with a square cross-section (side length \(d=20~\mathrm{mm}\)) is subjected to a tensile force \(F=10~\mathrm{kN}\) along the beam axis.
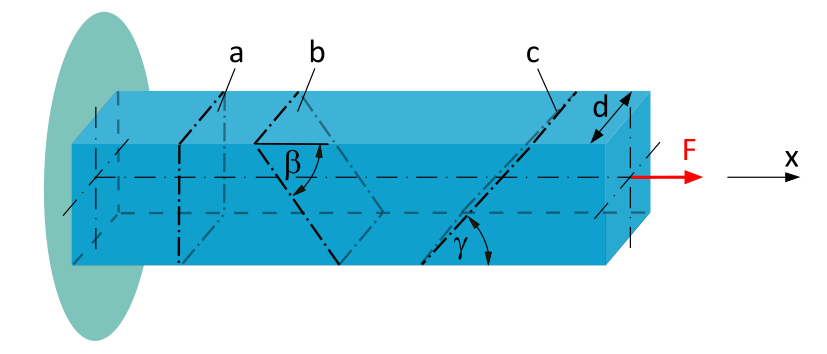
Determine the average normal stress and the average shear stress...
- ...acting in cross-sectional plane a.
- ...acting in cross-sectional plane b (\(\beta = 50°\)).
- ...acting in cross-sectional plane c (\(\gamma = 40°\)).
Short Solution
- Determine the average normal stress and the average shear stress acting in cross-sectional plane a.
- Determine the average normal stress and the average shear stress acting in cross-sectional plane a.
- Determine the average normal stress and the average shear stress acting in cross-sectional plane b (\(\beta = 50°\)).
- Determine the average normal stress and the average shear stress acting in cross-sectional plane b (\(\beta = 50°\)).
- Determine the average normal stress and the average shear stress acting in cross-sectional plane c (\(\gamma = 40°\)).
- Determine the average normal stress and the average shear stress acting in cross-sectional plane c (\(\gamma = 40°\)).
Comprehensive Solution
Preliminary Considerations
Ready to crack the stress state for different cutting angles in a beam? Cool stuff! Don't worry, it's a piece of cake.
First, take a deep breath and relax. The beam is loaded by a force \(F\) acting along its axis. This means we're dealing with a uniaxial stress state – easy peasy, right?
You'll need the following:
-
For a perpendicular cut to the beam axis:
$$ \begin{aligned} \sigma_x = \dfrac{N_x}{A} \end{aligned} $$
(1.3)
-
For an arbitrary cutting angle:
$$ \begin{aligned} \sigma_\xi &= \dfrac{\sigma_x}{2}\bigl(1+\cos(2\varphi)\bigr) \end{aligned} $$
(1.4)
$$ \begin{aligned} \tau_{\xi\eta} &= -\dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$(1.5xy)
$$ \begin{aligned} \tau_{\xi\eta} &= \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$(1.5xz)
- What type of loading is present? (Tensile, compressive, ...)
- What is the magnitude of the force?
- What is the cross-sectional area?
- At what angle is the cut made?
In the next step, we'll move on to the practical application.
- Determine the average normal stress and the average shear stress acting in the section plane a.
We are looking for the normal stress and shear stress in a perpendicular section to the beam axis. The general formula for normal stress is:
(1.3)
The shear stress must be \(0\) since the external force \(F\) in the perpendicular section can only cause normal force and not shear force.
Step 1: Determine the normal force
To calculate the normal force, we cut the beam at section a and represent the external force \(F\) and the internal normal force \(N\). As a reminder: On the positive, left side of the section, we represent \(N\) in the positive direction (towards the positive x-axis), while on the negative, right side of the section, we represent \(N\) in the negative direction (opposite to the direction of the positive x-axis).
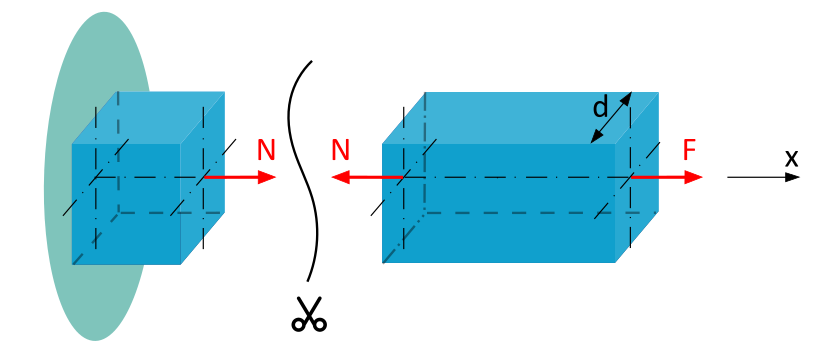
To save ourselves from calculating the support reactions (even though it's obvious that only one support reaction on the beam axis in the opposite direction of the x-axis and of magnitude \(F\) must act), we set up the horizontal equilibrium condition for the right section. This allows us to determine the normal force \(N\):
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for working alongside the semester with the content of TechMechAcademy.
- Unrestricted admission to all content, both pre-existing and recently generated, within the scope of the premium membership.
- Guaranteed premium membership for three months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the third month from the start date. No cancellation necessary.
€29.99
Overview of the benefits:
- Cost-effective due to extended duration.
- Ideal for semester preparation, concurrent semester work, and/or post-semester work with the content of TechMechAcademy.
- Unrestricted entry to a comprehensive collection of both existing and freshly generated content as part of the premium membership.
- Guaranteed premium membership for six months. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following day of the sixth month from the start date. No cancellation necessary.
€49.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.




