Übungsaufgabe F-1.1.4 TechMech 2 Festigkeitslehre

Vorherige Übungsaufgabe

Nächste Übungsaufgabe

Aufgabe F-1.1.4

Einachsiger Spannungszustand: Beliebiger Schnittwinkel

Aufgabenstellung

Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge $d=20~\mathrm{mm}$) wird wie in Abbildung 1 dargestellt durch eine Zugkraft $F=10~\mathrm{kN}$ in der Balkenachse belastet.

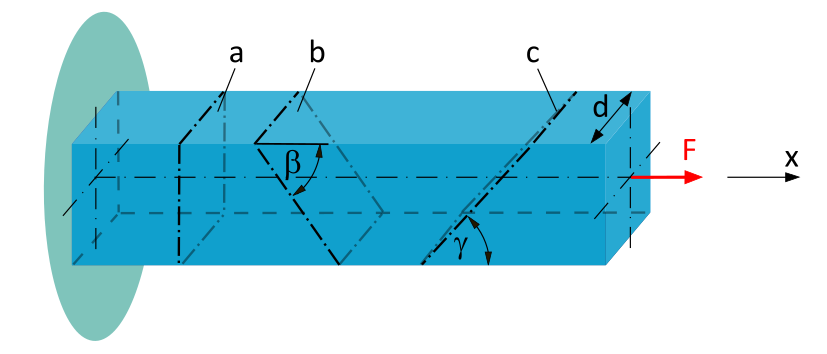
Die Abbildung zeigt einen linksseitig eingespannten Balken mit quadratischem Querschnitt. In der Zeichung sind drei Schnittebenen a, b und c angedeutet. Die Schnittebene a ist senkrecht zur Balkenachse. Die Schnittebene b verläuft von links oben nach rechts unten, der gegebene Winkel Beta beschreibt den kleineren Winkel oben. Die Schnittebene c verläuft von links unten nach rechts oben, der gegebene Winkel Gamma beschreibt den kleineren Winkel unten. Die Seitenlänge des Querschnittes ist die Länge d. Am rechten Balkenende wirkt eine Zugkraft F im Schwerpunkt des Querschnitts. — Abb. 1: Eingespannter Balken

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die

in der Schnittebene a wirken.
in der Schnittebene b ($\beta = 50°$) wirken.
in der Schnittebene c ($\gamma = 40°$) wirken.

Kurzlösung

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die in der Schnittebene a wirken.

$$ \begin{aligned} \sigma_a &= 25~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = 25~\mathrm{MPa}\\ \tau_a &= 0~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = 0~\mathrm{MPa} \end{aligned} $$

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die in der Schnittebene b ($\beta = 50°$) wirken.

$$ \begin{aligned} \sigma_b &= 14,671~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = 14,671~\mathrm{MPa}~(\nearrow)\\ \tau_b &= -12,310~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = -12,310~\mathrm{MPa}~(\nwarrow) \end{aligned} $$

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die in der Schnittebene c ($\gamma = 40°$) wirken.

$$ \begin{aligned} \sigma_c &= 10,329~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = 10,329~\mathrm{MPa}~(\searrow)\\ \tau_c &= 12,310~\dfrac{\mathrm{N}}{\mathrm{mm}^2 } = 12,310~\mathrm{MPa}~(\nearrow) \end{aligned} $$

Ausführlicher Lösungsweg

Vorüberlegungen

Du willst den Spannungszustand für verschiedene Schnittwinkel im Balken knacken? Coole Sache! Aber keine Sorge, es ist easy peasy.

Entspann dich erstmal! Der Balken wird durch eine Kraft $F$ belastet, deren Wirkungslinie die Balkenachse ist. Es liegt also ein einachsiger Spannungszustand vor – alles easy, oder?

Jetzt ist es an der Zeit, deine Formeln hervorzukramen.

Du wirst Folgendes benötigen:

Senkrechter Schnitt zur Balkenachse:

$$ \begin{aligned} \sigma_x = \dfrac{N_x}{A} \end{aligned} $$

(1.3)
Beliebiger Schnittwinkel:

$$ \begin{aligned} \sigma_\xi &= \dfrac{\sigma_x}{2}\bigl(1+\cos(2\varphi)\bigr) \end{aligned} $$

(1.4)

$$ \begin{aligned} \tau_{\xi\eta} &= -\dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$

(1.5_xy)

$$ \begin{aligned} \tau_{\xi\eta} &= \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$

(1.5_xz)

Bevor wir uns in die Berechnung stürzen, müssen wir ein paar wichtige Punkte klären:

Welche Art von Belastung liegt vor? (Zug, Druck, ...)
Wie groß ist die Kraft?
Wie groß ist die Querschnittsfläche?
In welchem Winkel wird geschnitten?

Das war's dann auch schon mit der Theorie.

Im nächsten Schritt geht's dann an die praktische Anwendung! ️

Also, ran an die Arbeit und viel Erfolg!

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die in der Schnittebene a wirken.

Wir suchen die Normalspannung und die Schubspannung in einem senkrechten Schnitt zur Balkenachse. Die allgemeine Formel für die Normalspannung lautet:

$$ \begin{aligned} \sigma_x = \dfrac{N_x}{A} \end{aligned} $$

(1.3)

Die Schubspannung muss $0$ sein, da die äußere Kraft $F$ im senkrechten Schnitt nur eine Normalkraft und keine Querkraft bewirken kann.

Schritt 1: Normalkraft bestimmen

Um die Normalkraft zu berechnen, schneiden wird den Balken an der Schnittebene a und tragen die äußere Kraft $F$ und die innere Normalkraft $N$ an. Zur Erinnerung: Am positiven, linken Schnittufer tragen wir $N$ in positiver (in Richtung der positiven x-Achse) Richtung an, am negativen, rechten Schnittufer hingegen in negativer (gegen die Richtung der positiven x-Achse) Richtung.

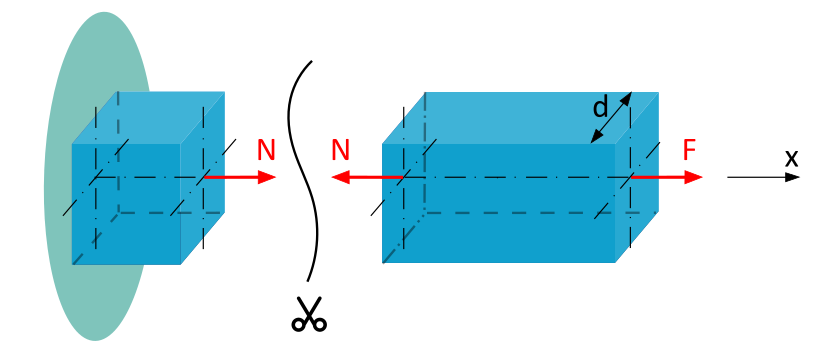
Diese Grafik zeigt den an der Schnittfläche a geschnittenen Balken mit der Schnittreaktion Normalkraft. — Abb. 2: Normalkraft an der Schnittfläche a bestimmen

Um uns die Berechnung der Lagerreaktionen zu sparen (auch wenn hier offensichtlich nur eine Lagerreaktion auf der Stabachse entgegen der x-Richtung in Größe der Kraft $F$ wirken muss), stellen wir die horizontale Gleichgewichtsbedingung für den rechten Schnitt auf. Damit können wir die Normalkraft $N$ bestimmen:

$$ \begin{align} \tag{1} \rightarrow: F - N &= 0\\[7pt] \tag{2} N &= \underline{F} \end{align} $$

Für Einsteiger: TechMechAcademy+. Voller Zugriff auf alle Inhalte für einen Tag.

Die Vorteile im Überblick:

Kostengünstigstes Angebot.
Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.

3,99 €

TechMechAcademy+. Voller Zugriff auf alle Inhalte für eine Woche.

Die Vorteile im Überblick:

Kostengünstiges Angebot.
Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
Unbeschränkter Zugang zu sämtlichen bestehenden und frisch erstellten Inhalten im Rahmen der gesamten Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.

9,99 €

Bestseller: TechMechAcademy+. Voller Zugriff auf alle Inhalte für einen Monat.

Die Vorteile im Überblick:

Profitiere vom Bestseller.
Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
Unlimitierter Zugriff auf alle bereits vorhandenen und neu geschaffenen Inhalte während der gesamten Dauer der Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.

14,99 €

TechMechAcademy+. Voller Zugriff auf alle Inhalte für drei Monate.

Die Vorteile im Überblick:

Kostengünstig durch lange Laufzeit.
Ideal für semesterbegleitendes Arbeiten mit den Inhalten von TechMechAcademy.
Freier Zugang zu sämtlichen bestehenden und neu erstellten Inhalten innerhalb der gesamten Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von drei Monaten gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des dritten Monats ab dem Startdatum. Keine Kündigung notwendig.

29,99 €

TechMechAcademy+. Voller Zugriff auf alle Inhalte für sechs Monate.

Die Vorteile im Überblick:

Kostengünstig durch lange Laufzeit.
Ideal für semestervorbereitendes, semesterbegleitendes und/oder semesternachbereitendes Arbeiten mit den Inhalten von TechMechAcademy.
Unbegrenzter Zugriff auf alle vorhandenen und neu geschaffenen Inhalte im Verlauf der kompletten Premiummitgliedschaft.
Die Premiummitgliedschaft ist für einen garantierten Zeitraum von sechs Monaten gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des sechsten Monats ab dem Startdatum. Keine Kündigung notwendig.

49,99 €

Werde ein TechMechAcademy+ Premiummitglied!

Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.