2. Berechnungsmethoden für beliebige Flächen
Im Folgenden werden wir die Berechnungsmethoden für die Flächenträgheitsmomente \(I_y\), \(I_z\) und \(I_{yz}\) für Flächen beliebiger Form unter Verwendung von kartesischen Koordinaten und Polarkoordinaten erläutern. Es stehen insgesamt sechs verschiedene Herangehensweisen zur Verfügung, von denen im folgenden vier näher vorgestellt und mit je einem Beispiel verdeutlicht werden. Welche davon genutzt werden sollte, hängt zum einen davon ab, wie wir das infinitesimale Flächenelement \(dA\), wie es in den Gleichungen (6.2) - (6.4) enthalten ist, konstruieren können und zum anderen, ob kartesische Koordinaten oder Polarkoordinaten verwendet werden.
2.1 Verwendung kartesischer Koordinaten
2.1.1 Infinitesimales Flächenelement
Wir arbeiten mit einem winzigen Flächenelement \(dA\), das die Seitenlängen \(dy\) und \(dz\) hat, wie in Abbildung 6.2.1 dargestellt.

Da dieses Flächenelement infinitesimal in beiden Koordinatenrichtungen ist, benötigen wir ein Doppelintegral, um die Berechnung durchzuführen:
(6.5)
Um diese Formel anwenden zu können, ist es erforderlich, den funktionalen Zusammenhang \(z(y)\) zu ermitteln. Sollte dies nicht möglich sein, besteht als alternative Option die Verwendung der Integrationsgrenzen \(z\) und \(y(z)\).
Beispiel 6.1: Bestimme Flächenträgheitsmoment für beliebige Flächen mit der Berechnungsmethode infinitesimales Flächenelement in kartesischen Koordinaten
Für die abgebildete Viertelkreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems unter Verwendung der Berechnungsmethode infinitesimales Flächenelement in kartesischen Koordinaten zu bestimmen:

- axiales Flächenträgheitsmoment \(I_y\)
- axiales Flächenträgheitsmoment \(I_z\)
- biaxiales Flächenträgheitsmoment \(I_{yz}\)
Lösung
Um die geforderte Berechnungsmethode anwenden zu können, ist es erforderlich, den funktionalen Zusammenhang \(z(y)\) zu ermitteln.
Diesen finden wir, wenn wir uns für den (Viertel-) Kreis den Zusammenhang von einem beliebigen Wert \(y\), dem dazugehörigen Wert \(z(y)\) und dem Radius des (Viertel-) Kreises verdeutlichen:

Wir erkennen ein rechtwinkliges Dreieck, und mithilfe des Satzes der Pythagoras erhalten wir die Kreisgleichung
Weiterlesen mit TechMechAcademy+
Alles. Immer. Überall.
Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.
Die Vorteile im Überblick:
- Kostengünstigstes Angebot.
- Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
- Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
- Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.
3,99 €
Die Vorteile im Überblick:
- Kostengünstiges Angebot.
- Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unbeschränkter Zugang zu sämtlichen bestehenden und frisch erstellten Inhalten im Rahmen der gesamten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.
9,99 €
Die Vorteile im Überblick:
- Profitiere vom Bestseller.
- Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unlimitierter Zugriff auf alle bereits vorhandenen und neu geschaffenen Inhalte während der gesamten Dauer der Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.
14,99 €
Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.

Flächenträgheitsmoment bestimmen
Für das abgebildete Rechteck sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)
Flächenträgheitsmoment bestimmen
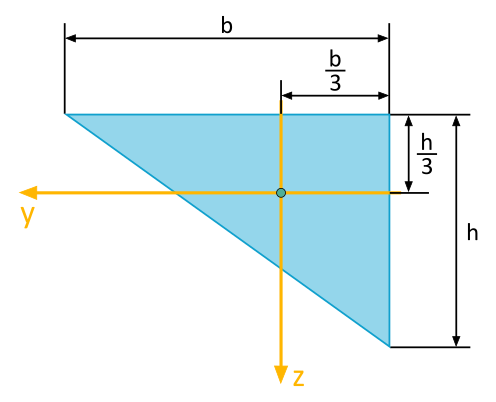
Für das abgebildete Dreieck sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)
Flächenträgheitsmoment bestimmen
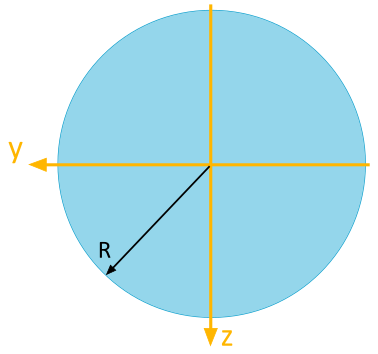
Für die abgebildete Kreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)


