2.1.2 Vertical Infinitesimal Area Strip
In Figure 6.2.2, instead of using a tiny area element \(\mathrm{d}A\) with side lengths \(\mathrm{d}y\) and \(\mathrm{d}z\) (Figure 6.2.1), we employ a vertically arranged, infinitesimal strip of thickness \(\mathrm{d}y\) parallel to the \(z\)-axis. This ensures that all points on the strip have the same \(y\)-coordinate with respect to the \(z\)-axis.
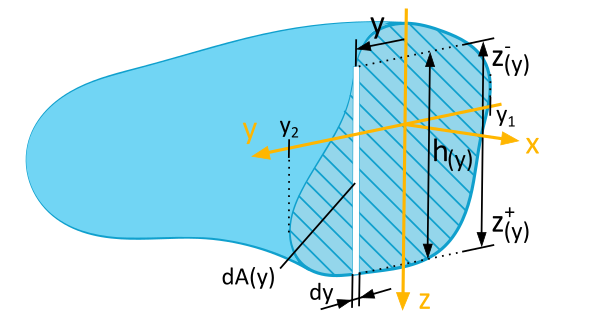
The height \(h(y)\) of the strip depends on the \(y\)-coordinate. Therefore, the calculation for the area element \(\mathrm{d}A\) in the formulas (6.2), (6.3) and (6.4) is given by
In order to perform the calculation of area moments of inertia using this method, it is necessary to determine the functional relationship \(h(y)\). This allows us to obtain the upper and lower bounding functions, which, for each \(y\), provide the upper \(\left(z^+(y)\right)\) and lower \(\left(z^-(y)\right)\) bounds of the area element.
Thus, for any arbitrary \(y\):
For any arbitrary \(y\), we can determine the infinitesimal area moments of inertia using the formulas (6.2) and (6.4) by utilizing equations (1) and (2) while keeping the independent variable \(y\) constant:
We obtain the sought area moments of inertia for the entire area by summing, or integrating, the infinitesimal quantities \(\mathrm{d}I_y(y)\), \(\mathrm{d}I_z(y)\), and \(\mathrm{d}I_{yz}(y)\) over the independent variable \(y\):
Compared to Formula (6.5), this calculation method essentially simplifies only Equation (7) for \(I_z\), since for the vertical strip, the following holds:
Thus, our result is
(6.6)
Example 6.2: Determining Area Moment of Inertia using the Calculation Method for Arbitrary Shapes Vertical Infinitesimal Area Strip in Cartesian Coordinates
For the quarter-circle area depicted, the following area moments of inertia with respect to the illustrated \(y\), \(z\)-coordinate system are to be determined using the calculation method vertical infinitesimal area strip in Cartesian coordinates:
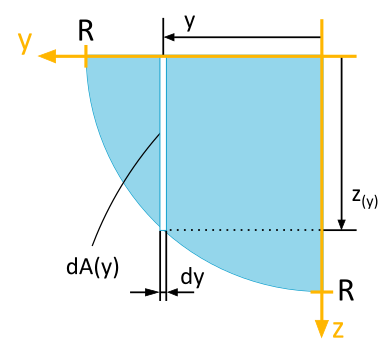
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
Solution
In order to apply the required calculation method, it is necessary to determine the functional relationship \(h(y) = z(y)\) and thus also the upper and lower bounding functions \(z^+(y)\) and \(z^-(y)\).
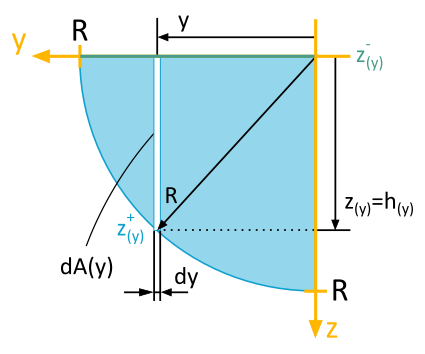
As shown in Fig. B6.2.2, the lower bounding function is
, which corresponds to the \(y\)-axis.
Continue with TechMechAcademy+
Everything. Always. Everywhere.
With TechMechAcademy+ full access to all content.
Overview of the benefits:
- Most cost-effective offer.
- Ideal if you need access to already identified content for a short period.
- Unlimited access to all existing and newly created content throughout the entire premium membership.
- Guaranteed premium membership for 24 hours. Access automatically ends at 0:00 CET (Central European Time) on the following day. No cancellation necessary.
€3.99
Overview of the benefits:
- Cost-effective offer.
- Ideal for short-term exam preparation with the content of TechMechAcademy.
- Unrestricted entry to every piece of content, both existing and newly generated, across the entirety of the premium membership.
- Guaranteed premium membership for one week. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following week's day. No cancellation necessary.
€9.99
Overview of the benefits:
- Benefit from the bestseller.
- Ideal for effective exam preparation with the content of TechMechAcademy.
- Complete access to all content, both existing and newly produced, under the umbrella of the premium membership.
- Guaranteed premium membership for one month. Access starts on the day of activation and ends automatically at 0:00 CET (Central European Time) on the following month's day. No cancellation necessary.
€14.99
Are you already a TechMechAcademy+ premium member? Then please log in here to enjoy full access to all content.
Determine the Area Moment of Inertia
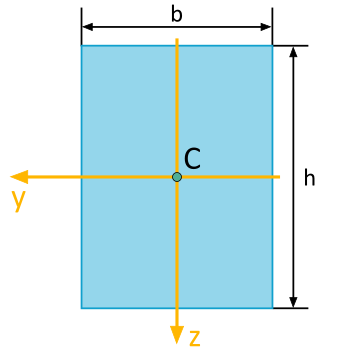
For the rectangle area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
Determine the Area Moment of Inertia
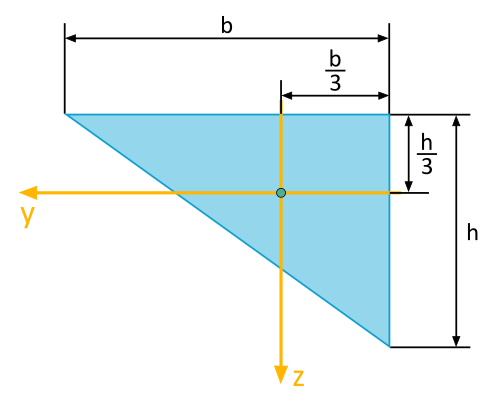
For the triangle area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)
Determine the Area Moment of Inertia
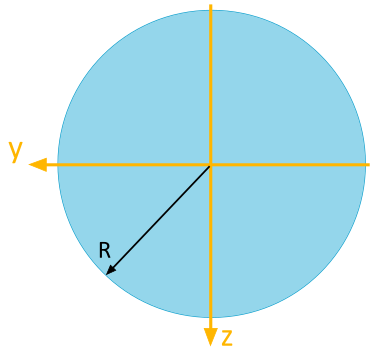
For the circular area depicted, the following area moments of inertia are to be determined with respect to the illustrated \(y\), \(z\)-coordinate system:
- Axial Area Moment of Inertia \(I_y\)
- Axial Area Moment of Inertia \(I_z\)
- Biaxial Area Moment of Inertia \(I_{yz}\)


