2.1.2 Vertikaler infinitesimaler Flächenstreifen
In Abbildung 6.2.2 verwenden wir anstelle eines winzigen Flächenelements \(\mathrm{d}A\), das die Seitenlängen \(\mathrm{d}y\) und \(\mathrm{d}z\) hat (Abbildung 6.2.1), einen vertikal angeordneten, infinitesimalen Flächenstreifen der Dicke \(\mathrm{d}y\), der parallel zur \(z\)-Achse verläuft. Dadurch haben alle Punkte auf dem Streifen dieselbe \(y\)-Koordinate in Bezug zur \(z\)-Achse.
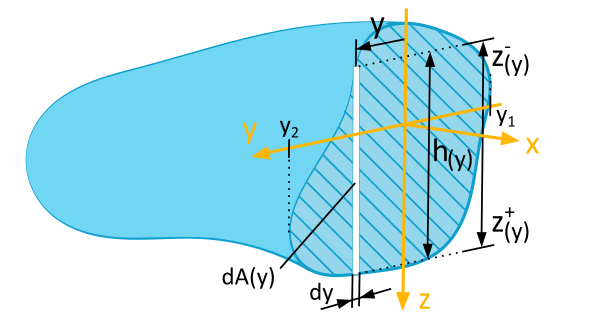
Die Höhe \(h(y)\) des Flächenstreifens hängt von der \(y\)-Koordinate ab. Daher ergibt sich für das Flächenelement \(\mathrm{d}A\) in den Formeln (6.2), (6.3) und (6.4) die Berechnung
Um die Berechnung der Flächenträgheitsmomente mit dieser Methode durchführen zu können, ist es erforderlich, dass die funktionale Beziehung \(h(y)\) ermittelt werden kann. Damit erhalten wir die obere und untere Begrenzungsfunktion, die für jedes \(y\) die obere \(\left(z^+(y)\right)\) und untere \(\left(z^-(y)\right)\) Begrenzung des Flächendifferentiales liefert.
Damit gilt für jedes beliebige y:
Wir können damit für jedes beliebige \(y\) die infinitesimalen Flächenträgheitsmomente nach den Formeln (6.2) und (6.4) bestimmen, indem wir die Gleichungen (1) und (2) nutzen und die unabhängige Variable \(y\) konstant halten:
Wir erhalten die gesuchten Flächenträgheitsmomente für die gesamte Fläche, indem wir die infinitesimalen Größen \(\mathrm{d}I_y(y)\), \(\mathrm{d}I_z(y)\) und \(\mathrm{d}I_{yz}(y)\) über die unabhängige Variable \(y\) aufsummieren, also integrieren:
Im Vergleich zur Formel (6.5) vereinfacht sich durch diese Berechnungsmethode im Grunde nur die Gleichung (7) für \(I_z\), da für den vertikalen Flächenstreifen gilt:
Wir erhalten also als Ergebnis
(6.6)
Beispiel 6.2: Bestimme Flächenträgheitsmoment für beliebige Flächen mit der Berechnungsmethode vertikaler infinitesimaler Flächenstreifen in kartesischen Koordinaten
Für die abgebildete Viertelkreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems unter Verwendung der Berechnungsmethode vertikaler infinitesimaler Flächenstreifen in kartesischen Koordinaten zu bestimmen:
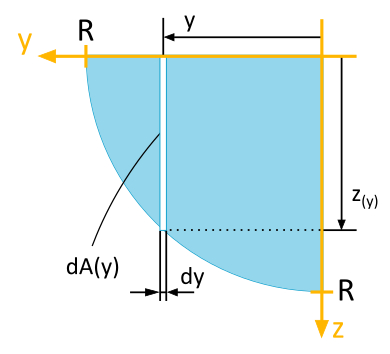
- axiales Flächenträgheitsmoment \(I_y\)
- axiales Flächenträgheitsmoment \(I_z\)
- biaxiales Flächenträgheitsmoment \(I_{yz}\)
Lösung
Um die geforderte Berechnungsmethode anwenden zu können, ist es erforderlich, den funktionalen Zusammenhang \(h(y) = z(y)\) und damit auch die obere und untere Begrenzungsfunktion \(z^+(y)\) und \(z^-(y\)) zu ermitteln.
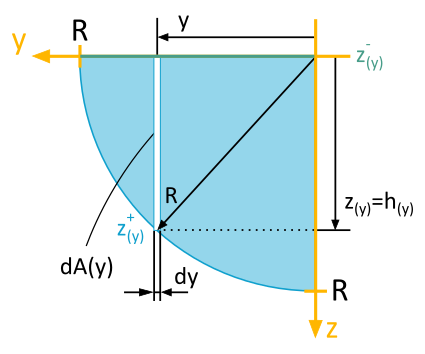
Wie in Abb. B6.2.2 zu sehen, ist die untere Begrenzungsfunktion
, also die \(y\)-Achse.
Weiterlesen mit TechMechAcademy+
Alles. Immer. Überall.
Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.
Die Vorteile im Überblick:
- Kostengünstigstes Angebot.
- Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
- Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
- Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.
3,99 €
Die Vorteile im Überblick:
- Kostengünstiges Angebot.
- Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unbeschränkter Zugang zu sämtlichen bestehenden und frisch erstellten Inhalten im Rahmen der gesamten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.
9,99 €
Die Vorteile im Überblick:
- Profitiere vom Bestseller.
- Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unlimitierter Zugriff auf alle bereits vorhandenen und neu geschaffenen Inhalte während der gesamten Dauer der Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.
14,99 €
Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.

Flächenträgheitsmoment bestimmen
Für das abgebildete Rechteck sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)
Flächenträgheitsmoment bestimmen
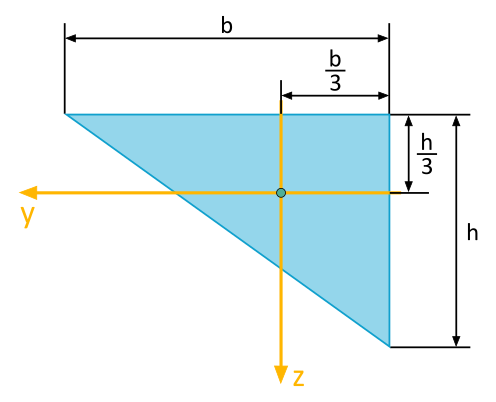
Für das abgebildete Dreieck sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)
Flächenträgheitsmoment bestimmen
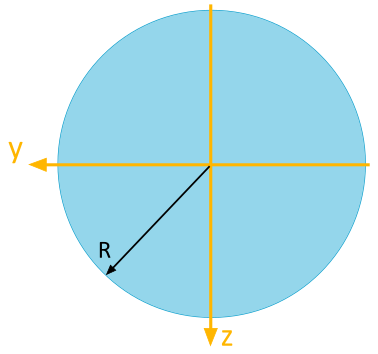
Für die abgebildete Kreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten \(y\), \(z\)-Koordinatensystems zu bestimmen:
- Axiales Flächenträgheitsmoment \(I_y\)
- Axiales Flächenträgheitsmoment \(I_z\)
- Biaxiales Flächenträgheitsmoment \(I_{yz}\)


