Uniaxial State of Stress - Any Section Angle, Step 1

Normal and Shear Stresses at an Arbitrary Angle

Step 2: Determining the Normal Force $N_\xi$ as a Function of the Angle $\varphi$

On this Page

Practice Exercises

Table of Contents

Step 1: Determining the Cross-Sectional Area $A^*$ as a Function of the Cutting Angle $\varphi$

Slice and Dice with Angles

Ready for some geometry fun?

Today, we're going to explore the cross-sectional area $A^*$, but not just any area, the area as a function of the cutting angle $\varphi$. Sounds complicated? It's not, I promise!

First, let's sketch two cross-sections: a perpendicular one and an arbitrary, oblique one.

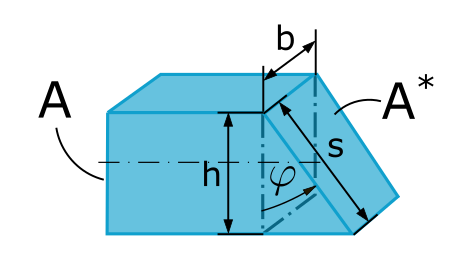
This figure shows the dimensioning of the cross-sectional area A* with the width b and length s, as well as the dimensioning of the cross-sectional area of the perpendicular cut A with the width b and height h. — Fig. 1.2.8: Determination of the Cross-Sectional Area $A^*$

$A$ and $A^*$ look like rectangles, and we can calculate their areas with the formulas:

$$ \begin{alignat}{3} \tag{1} A &= h \cdot b && \quad\text{(perpendicular)}\\[10pt] \tag{2} A^* &= s \cdot b && \quad\text{(oblique)} \end{alignat} $$

But wait! The oblique area $A^*$ depends on the angle $\varphi$. The more oblique the cut, the larger or smaller the area becomes.

How do we find the connection?

Easy peasy with a triangle!

This figure shows a triangle with the height h of the perpendicular cross-section, the length s of the arbitrary cross-section, and the angle Phi. — Fig. 1.2.9: Geometric Relationships at the Cross-Section

The height of the triangle is $h$ (the length of the perpendicular cross-section), the hypotenuse is $s$ (the length of the oblique cross-section), and the angle $\varphi$ is, well... the cutting angle $\varphi$.

Using trigonometry (yes, I know, math) we can calculate $s$ as a function of $\varphi$:

$$ \begin{align} \tag{3} \cos(\varphi) &= \dfrac{\mathrm{adjacent}}{\mathrm{hypotenuse}}\\[10pt] \tag{4} \cos(\varphi) &= \dfrac{h}{s} \end{align} $$

This allows us to express $s$ as:

$$ \begin{align} \tag{5} s = \dfrac{h}{\cos(\varphi)} \end{align} $$

What's that?

Don't worry, it's just the cosine! It tells us the length of the hypotenuse ($s$) relative to the adjacent side ($h$).

Now we have everything we need!

The cross-sectional area $A^*$ as a function of $\varphi$:

$$ \begin{align} \tag{6} A^* = s \cdot b = \dfrac{h}{\cos(\varphi)} \cdot b \end{align} $$

Remember:

$A^*$ gets larger when you cut more obliquely (larger $\varphi$ $\Rightarrow$ smaller $\cos\varphi)$).
$A^*$ gets smaller when you cut more perpendicularly (smaller $\varphi$ $\Rightarrow$ larger $\cos(\varphi)$).

By the way:

If we combine the product $h \cdot b = A$, we can express $A^*$ as:

$$ \begin{aligned} A^* = \dfrac{A}{\cos(\varphi)} \end{aligned} $$

(7)

Practice Exercise

Practice Exercise F-1.1.4

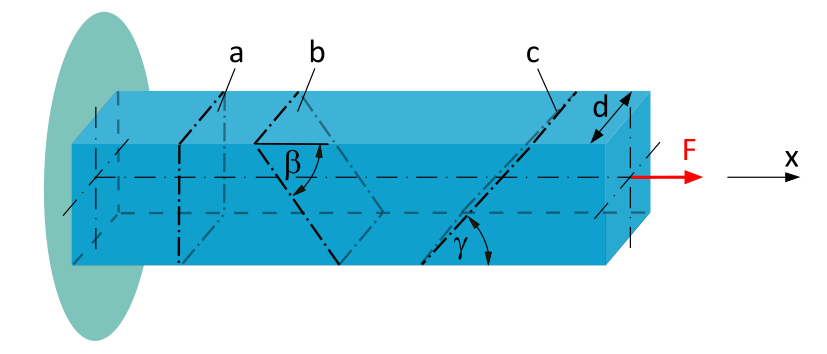
The illustration shows a beam with a square cross-section, fixed on the left side. In the drawing, three sectional planes a, b, and c are indicated. Sectional plane a is perpendicular to the beam axis. Sectional plane b runs from the upper left to the lower right, with the given angle Beta describing the smaller angle at the top. Sectional plane c runs from the lower left to the upper right, with the given angle Gamma describing the smaller angle at the bottom. The side length of the cross-section is denoted as d. A tensile force F acts at the right end of the beam at the center of the cross-section.

Normal and Shear Stress at an Arbitrary Section Angle

A clamped beam with a square cross-section (side length $d=20~\mathrm{mm}$) is subjected to a tensile force $F=10~\mathrm{kN}$ along the beam axis.

Determine the average normal stress and the average shear stress...

...acting in cross-sectional plane a.
...acting in cross-sectional plane b ($\beta = 50°$).
...acting in cross-sectional plane c ($\gamma = 40°$).

Mechanics of Materials

Stress State: Dive into the World of Forces and Stresses!

Step 1: Determining the Cross-Sectional Area \(A^*\) as a Function of the Cutting Angle \(\varphi\)

Normal and Shear Stress at an Arbitrary Section Angle