Einachsiger Spannungszustand - Beliebiger Schnittwinkel I

Normal- und Schubspannungen unter einem beliebigen Schnittwinkel

Schritt 2: Normalkraft $N_\xi$ als Funktion des Schnittwinkels $\varphi$ bestimmen

Auf dieser Seite

Übungsaufgaben

Inhaltsverzeichnis

Schritt 1: Schnittfläche $A^*$ als Funktion des Schnittwinkels $\varphi$ bestimmen

Schnittfläche $A^*$ - Winkelspielereien

Bereit für ein bisschen Geometrie-Spaß?

Jetzt geht's um die Schnittfläche $A^*$. Aber nicht einfach so, nein, als Funktion des Schnittwinkels $\varphi$. Klingt kompliziert? Ist es aber nicht!

Zuerst skizzieren wir zwei Schnittflächen: eine senkrechte und eine beliebige, schräge.

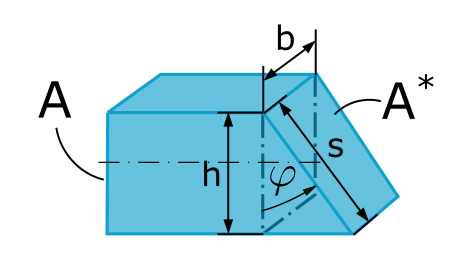
Diese Abbildung zeigt die Bemaßung der Schnittfläche A* mit der Breite b und der Länge s, zudem die Bemaßung der Schnittfläche des senkrechten Schnitts A mit der Breite b und der Höhe h. — Abb. 1.2.8: Bestimmung der Schnittfläche $A^*$

Die Schnittflächen sehen aus wie Rechtecke, und wir berechnen sie mit

$$ \begin{alignat}{3} \tag{1} A &= h \cdot b && \quad\text{(senkrecht)}\\[10pt] \tag{2} A^* &= s \cdot b && \quad\text{(schräg)} \end{alignat} $$

Aber Achtung! Die schräge Fläche $A^*$ hängt vom Winkel $\varphi$ ab. Je nachdem, wie schräg du schneidest, wird die Fläche also größer oder kleiner.

Wie kriegen wir den Zusammenhang raus?

Ganz einfach: Mithilfe eines Dreiecks!

Diese Abbildung zeigt ein Dreieck aus der Höhe h der senkrechten Schnittfläche, der Länge s der beliebigen Schnittfläche und des Schnittwinkels Phi. — Abb. 1.2.9: Geometrische Beziehungen an der Schnittfläche

Die Höhe des Dreiecks ist $h$ (die Länge der senkrechten Schnittfläche), die Hypotenuse ist $s$ (die Länge der schrägen Schnittfläche) und der Winkel $\varphi$ ist natürlich... der Schnittwinkel $\varphi$.

Mit Trigonometrie (ja, ich weiß, Mathe) können wir $s$ als Funktion von $\varphi$ berechnen:

$$ \begin{align} \tag{3} \cos(\varphi) &= \dfrac{\mathrm{Ankathete}}{\mathrm{Hypotenuse}}\\[10pt] \tag{4} \cos(\varphi) &= \dfrac{h}{s} \end{align} $$

Damit können wir $s$ ausdrücken als

$$ \begin{align} \tag{5} s = \dfrac{h}{\cos(\varphi)} \end{align} $$

Huch, was ist das denn?

Keine Angst, nur ein bisschen Kosinus! Er sagt uns, wie lang die Hypotenuse ($s$) im Verhältnis zur Ankathete ($h$) ist.

Jetzt haben wir alles, was wir brauchen!

Die Schnittfläche $A^*$ als Funktion von $\varphi$:

$$ \begin{align} \tag{6} A^* = s \cdot b = \dfrac{h}{\cos(\varphi)} \cdot b \end{align} $$

Merke dir:

$A^*$ wird größer, wenn du schräger schneidest (größerer $\varphi$ $\Rightarrow$ kleinerer $\cos\varphi)$).
$A^*$ wird kleiner, wenn du senkrechter schneidest (kleinerer $\varphi$ $\Rightarrow$ größerer $\cos(\varphi)$).

Übrigens:

Wenn wir jetzt noch das Produkt $h \cdot b = A$ zusammenfassen, können wir $A^*$ ausdrücken als

$$ \begin{aligned} A^* = \dfrac{A}{\cos(\varphi)} \end{aligned} $$

(7)

Übungsaufgabe

Aufgabe F-1.1.4

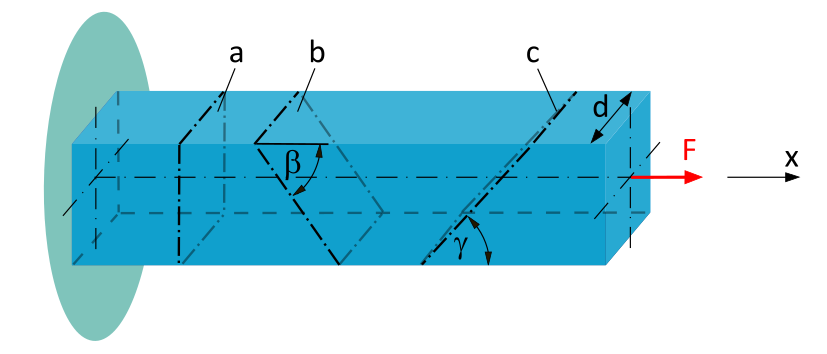
Die Abbildung zeigt einen linksseitig eingespannten Balken mit quadratischem Querschnitt. In der Zeichung sind drei Schnittebenen a, b und c angedeutet. Die Schnittebene a ist senkrecht zur Balkenachse. Die Schnittebene b verläuft von links oben nach rechts unten, der gegebene Winkel Beta beschreibt den kleineren Winkel oben. Die Schnittebene c verläuft von links unten nach rechts oben, der gegebene Winkel Gamma beschreibt den kleineren Winkel unten. Die Seitenlänge des Querschnittes ist die Länge d. Am rechten Balkenende wirkt eine Zugkraft F im Schwerpunkt des Querschnitts.

Normal- und Schubspannung unter beliebigem Schnittwinkel

Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge $d=20~\mathrm{mm}$) wird durch eine Zugkraft $F=10~\mathrm{kN}$ in der Balkenachse belastet.

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die

in der Schnittebene a wirken.
in der Schnittebene b ($\beta = 50°$) wirken.
in der Schnittebene c ($\gamma = 40°$) wirken.

Festigkeitslehre / Elastostatik

Spannungszustand: Tauche ein in die Welt der Kräfte und Spannungen!

Schritt 1: Schnittfläche \(A^*\) als Funktion des Schnittwinkels \(\varphi\) bestimmen

Normal- und Schubspannung unter beliebigem Schnittwinkel