Step 2 | TechMechAcademy

Stress State: Dive into the World of Forces and Stresses!

Are you ready for an exciting journey into the world of physics? Then buckle up and discover the secrets of the stress state with us!

What is stress? Imagine you are building a giant Lego structure. The individual blocks push and pull against each other - that's exactly what stress is! In this course, you will learn how to calculate and understand these forces.

Stress components: Break down stress into its individual parts and discover how they interact. Just as a puzzle consists of many pieces, stress is also made up of different components.

Calculation: Crack the code of stress calculation! With a few clever formulas and tools, you can determine the forces in any component.

Transformation: Stresses change depending on the perspective. Learn how to transform them into different cutting planes and thus make the whole story of the load in the component visible.

Maximum stresses: Where does the greatest danger lurk? Find out where the stresses are highest in the component and how you can minimize them.

Mohr's circle of stress: This ingenious tool helps you to visualize stresses and to grasp important information at a glance.

Discover the fascination of the stress state! In this course you will not only learn dry knowledge, but also immerse yourself in the world of engineering. With good explanations and exciting application examples, the stress state becomes child's play.

Together we are strong! We will accompany you on your journey and help you to understand the complex concepts of the stress state. With our support you will master every challenge and become an expert for stable constructions.

So what are you waiting for? Start your journey into the world of stress now!

Step 1: Determining the Cross-Sectional Area $A^*$ as a Function of the Cutting Angle $\varphi$

Step 3: Determining the Shear Force $Q_\eta$ as a Function of the Angle $\varphi$

On this Page

Practice Exercises

Table of Contents

Step 2: Determining the Normal Force $N_\xi$ as a Function of the Angle $\varphi$

Crack the code of the normal force with the cosine trick!

Buckle up! In this step, we embark on an exciting journey into the world of trigonometry and reveal the true identity of the normal force $N_\xi$ using the cosine trick.

First, let's take a close look at the force triangle in Figure 1.2.10. A trigonometric relationship is hidden there between the angle $\varphi$, the normal force in $\xi$-direction $N_\xi$, and the normal force in x-direction $N_x$.

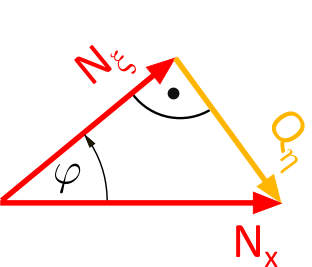
This figure shows an enlarged force triangle from Figure 1.2.5 consisting of N x, N Xi, and Q Eta. — Fig. 1.2.10: Force triangle from Figure 1.2.5

Imagine $N_\xi$ is a shy detective hiding behind $N_x$. But with the cosine trick, we can unmask him!

The Cosine Spell:

Known: Angle $\varphi$ and hypotenuse $N_x$
Wanted: Cathetus $N_\xi$

Magic Formula:

$$ \begin{align} \tag{1} \cos(\varphi) &= \frac{\text{Adjacent Side}}{\text{Hypotenuse}}\\[10pt] \tag{2} \cos(\varphi) &= \dfrac{N_\xi}{N_x} \end{align} $$

Hocus Pocus!

With a little bit of rearranging, we have:

$$ \begin{aligned} N_\xi = N_x \cdot \cos(\varphi) \end{aligned} $$

(3)

Aha! The normal force $N_\xi$ s proportional to the x-component $N_x$ and the cosine of the angle $\varphi$. The larger the angle, the more $N_\xi$ dares to come out of hiding. But: Since $\cos(\varphi)$ decreases with increasing $\varphi$, $N_\xi$ also decreases ab.

Remember:

Formula (3) is your magic key to calculating the normal force $N_\xi$.
Angle $\varphi$ and force $N_x$ are the ingredients for the magic potion.
With the cosine trick, you can unmask the secret identity of the normal force!

Have fun casting spells!

P.S.: If you need more magic, take a closer look at the trigonometric relationships.

P.P.S.: Don't forget that $N_\xi$ can be positive or negative. Depending on the direction of the force.

Practice Exercise

Practice Exercise F-1.1.4

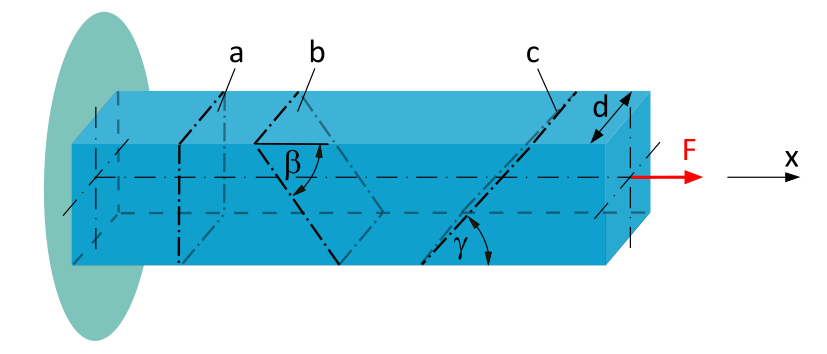
The illustration shows a beam with a square cross-section, fixed on the left side. In the drawing, three sectional planes a, b, and c are indicated. Sectional plane a is perpendicular to the beam axis. Sectional plane b runs from the upper left to the lower right, with the given angle Beta describing the smaller angle at the top. Sectional plane c runs from the lower left to the upper right, with the given angle Gamma describing the smaller angle at the bottom. The side length of the cross-section is denoted as d. A tensile force F acts at the right end of the beam at the center of the cross-section.

Normal and Shear Stress at an Arbitrary Section Angle

A clamped beam with a square cross-section (side length $d=20~\mathrm{mm}$) is subjected to a tensile force $F=10~\mathrm{kN}$ along the beam axis.

Determine the average normal stress and the average shear stress...

...acting in cross-sectional plane a.
...acting in cross-sectional plane b ($\beta = 50°$).
...acting in cross-sectional plane c ($\gamma = 40°$).

Mechanics of Materials

Stress State: Dive into the World of Forces and Stresses!

Step 2: Determining the Normal Force \(N_\xi\) as a Function of the Angle \(\varphi\)

Normal and Shear Stress at an Arbitrary Section Angle