Step 3: Determining the Shear Force \(Q_\eta\) as a Function of the Angle \(\varphi\)
Hey math enthusiasts, ready for a little scavenger hunt? We're chasing down the shear force \(Q_\eta\), but it's hiding behind the tricky angle \(\varphi\).
Don't worry, I'm your trusty sidekick! Together, we'll crack the code and unveil the secret formula.
-
Cheat sheet: Grab our genius stress triangle from Figure 1.2.10. It has everything we need!
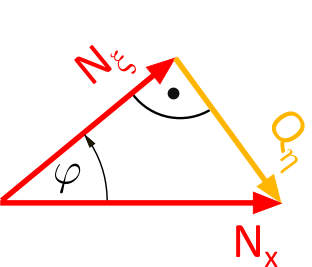
Fig. 1.2.10: Force triangle from Figure 1.2.5 - Decode the secret message: Take a close look at the opposite side \(Q_\eta\) and the hypotenuse \(N_x\). What do you notice? Aha! There's a trigonometric relationship hiding there!
-
Formula magic: With some sine magic and the equation
$$ \begin{align} \tag{1} \sin(\varphi) &= \dfrac{\mathrm{Opposite}}{\mathrm{Hypotenuse}}\\[10pt] \tag{2} \sin(\varphi) &= \dfrac{Q_\eta}{N_x} \end{align} $$we lure the shear force out of its hiding place. Tadaaa!
-
Mission accomplished! Now you have the formula for \(Q_\eta\) in your pocket:
$$ \begin{aligned} Q_\eta = N_x \cdot \sin(\varphi) \end{aligned} $$
(3)
Exciting, right? With this formula, you can calculate the shear force no matter what angle the sneaky \(\varphi\) throws at you.
By the way: This formula is brilliant, but not infallible. Don't forget to keep an eye on the units!
P.S.: If you need more math action, check out the trigonometric relationships. There are even more exciting secrets to uncover!
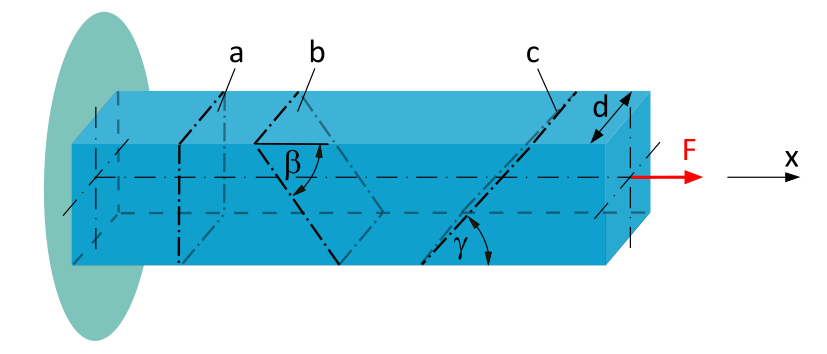
Normal and Shear Stress at an Arbitrary Section Angle
A clamped beam with a square cross-section (side length \(d=20~\mathrm{mm}\)) is subjected to a tensile force \(F=10~\mathrm{kN}\) along the beam axis.
Determine the average normal stress and the average shear stress...
- ...acting in cross-sectional plane a.
- ...acting in cross-sectional plane b (\(\beta = 50°\)).
- ...acting in cross-sectional plane c (\(\gamma = 40°\)).