7. Third Basic Task: Decomposition of a Force
Imagine you have a force R acting on a line. How cool would it be to split this force into two smaller "partial forces" F1 and F2 that act on two other lines? That's exactly what force decomposition is all about!
But don't worry, you don't need to be a physics genius for this! With a little understanding and the right formulas, you can do it in no time.
Take a look at Figure 3.7.1:
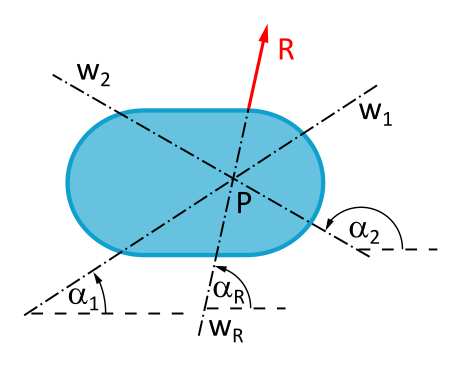
You see the force R on its line of action wR, with its angle \(\alpha_R\). There are also two other angles \(\alpha_1\) and \(\alpha_2\) for the lines of action w1 and w2.
Our goal: We want to find the components of the forces F1 and F2 on the lines of action w1 and w2 in Cartesian coordinates. This way we can later say that F1 and F2 together act exactly like the force R (this is then called "equivalent").
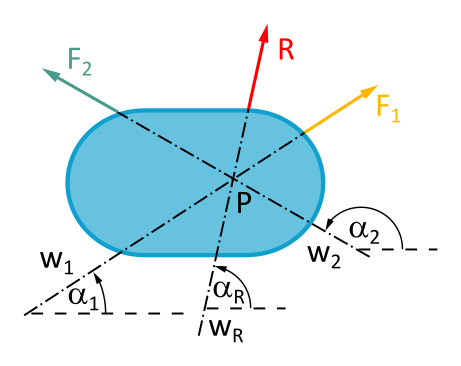
We have already worked out the relationship between the components of R, F1 and F2 here.
Using equations (2.4), you can calculate the magnitudes R, F1 and F2 if you know the angles \(\alpha_R\), \(\alpha_1\) and \(\alpha_2\):
Remember: If you substitute the angles as shown in Figures 3.7.1 and 3.7.2 into equations (1) and (2), you get the components of the force vectors with the correct sign. So positive if the component acts in the direction of an axis of the coordinate system, and negative if it acts against the direction of an axis.
Why? Look at the explanations of the angle functions on the unit circle. Then you will understand why in 2D the sine is positive in the I. and II. quadrant of the coordinate system (positive y-axis) and the cosine is positive in the I. and IV. quadrant (positive x-axis).
But enough thinking, back to the task:
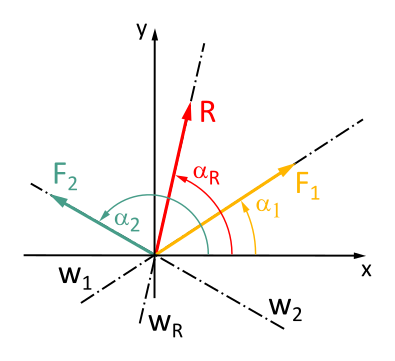
Let's save the math, here are the formulas:
(2.8)
Want to know more? Feel free, but at your own risk!
How to calculate F1: First take equations (1) and (2) from above. Multiply equation (1) with \(\sin \alpha_2\) and equation (2) with \(\cos \alpha_2\).
Now subtract equation (4) from equation (3):
With the trigonometric identity \(\sin(\varphi_1-\varphi_2) = \sin(\varphi_1) \cdot \cos(\varphi_2) - \cos(\varphi_1) \cdot \sin(\varphi_2)\):
And finally \(\sin 0 = 0\) remains:
How to calculate F2: Likewise, take equations (1) and (2) from above. Multiply equation (1) with \(\sin \alpha_1\) and equation (2) with \(\cos \alpha_1\).
Now subtract equation (9) from equation (8):
With the trigonometric identity \(\sin(\varphi_1-\varphi_2) = \sin(\varphi_1) \cdot \cos(\varphi_2) - \cos(\varphi_1) \cdot \sin(\varphi_2)\):
And finally \(\sin 0 = 0\) remains:
Because \(\sin(-\varphi)=-\sin(\varphi)\) we can also write:
In the realm of force decomposition, we're about to embark on a journey into the third dimension, where the z-axis joins the party. This means our force to be decomposed, R, now has three components: x, y, and z. This allows us to split a three-dimensional force R into three "partial forces" F1, F2 and F3.
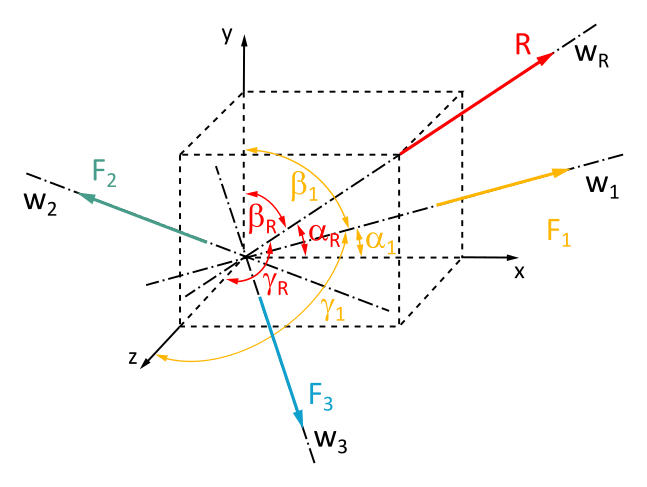
In this 3D graphic, the direction angle of a vector to the x-axis is denoted by \(\alpha\), the direction angle to the y-axis by \(\beta\), and the direction angle to the z-axis by \(\gamma\).
If you know the three direction angles of R (\(\alpha_R\), \(\beta_R\) and \(\gamma_R\)) and the direction angles of the lines of action w1 (\(\alpha_1\), \(\beta_1\) and \(\gamma_1\)), w2 (\(\alpha_2\), \(\beta_2\) and \(\gamma_2\)) and w3 (\(\alpha_3\), \(\beta_3\) and \(\gamma_3\)), then you get an equation for each component:
This set of equations forms a system of three equations with three unknowns: F1, F2 and F3.
(2.9)
This system of equations (2.9) can be solved using various methods, such as Gaussian elimination or Cramer's rule.
The system has a unique solution if the three lines of action of the vectors are not coplanar. This means that the three vectors do not lie in the same plane but span a three-dimensional space.
So, you've mastered the art of decomposing a force into multiple "partial forces" acting in different directions.
The number of directions you choose depends on whether you're in a plane or in space:
- Plane: Here, you can decompose the force into exactly two directions.
- Space: In the 3D universe, it's exactly three directions.
The cool thing: In both cases, the decomposition is unique. This means there is only one correct solution!
But beware: More directions, more possibilities! If you want to decompose the force into more than two or three directions, it gets tricky. Then there are infinitely many ways to do so.
Is that bad? Not necessarily! Sometimes it's even very practical to have multiple decompositions. For example, you can distribute the force on different parts of a construction.
Important, however: No matter how many directions you choose, the sum of the partial forces must always be equal to the main force. And the directions of the partial forces must be chosen so that together they result in the direction of the main force.
Force decomposition is that simple! With a little practice and the right tips, you can do it in no time.
A force F = 25 N is to be decomposed into two components F1 and F2 which are perpendicular to each other. The lines of action of F and F1 are to form an angle \(\alpha = 35°\).
Determine the magnitudes of F1 and F2 graphically and analytically.
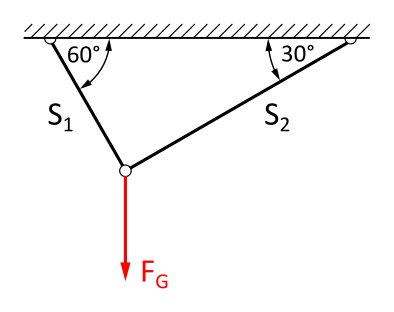
A mass with the weight force FG is hanging on two ropes.
What are the components of the force FG = 10 kN in the direction of ropes 1 and 2?
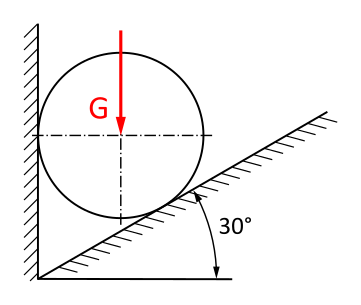
A sphere is situated, as shown, in a recess.
What are the components of the weight force G = 40 kN in the direction of the walls?
Note:
Only forces normal (i.e., perpendicular) to the wall can be transmitted.