7. Dritte Grundaufgabe: Zerlegung einer Kraft
Stell dir vor, du hast eine Kraft R, die auf einer Linie wirkt. Wie cool wäre es, diese Kraft in zwei kleinere "Teilkräfte" F1 und F2 aufzuteilen, die auf zwei anderen Linien wirken? Genau das ist das Ziel der Kraftzerlegung!
Aber keine Sorge, du brauchst dafür kein Physikgenie zu sein! Mit ein bisschen Verständnis und den richtigen Formeln schaffst du das im Handumdrehen.
Schau dir Abbildung 3.7.1 an:
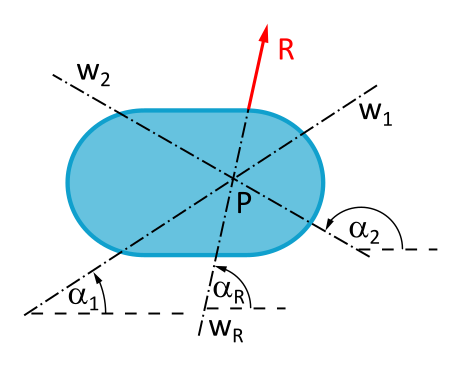
Da siehst du die Kraft R auf ihrer Wirkungslinie wR, mit ihrem Winkel \(\alpha_R\). Außerdem sind da noch zwei weitere Winkel \(\alpha_1\) und \(\alpha_2\) für die Wirkungslinien w1 und w2 eingezeichnet.
Unser Ziel: Wir wollen die Komponenten der Kräfte F1 und F2 auf den Wirkungslinien w1 und w2 in kartesischen Koordinaten herausfinden. So können wir später sagen, dass F1 und F2 zusammen genau so wirken wie die Kraft R (das nennt man dann "äquivalent").
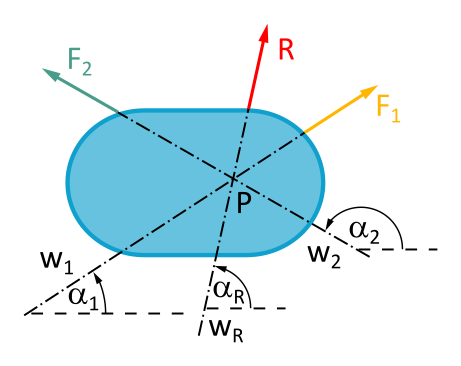
Den Zusammenhang zwischen den x- und y-Komponenten von R, F1 und F2 haben wir hier schon einmal herausgearbeitet.
Mithilfe der Gleichungen (2.4) kannst du die Größen R, F1 und F2 berechnen, wenn du die Winkel \(\alpha_R\), \(\alpha_1\) und \(\alpha_2\) kennst:
Denke daran: Wenn du die Winkel wie in Abb. 3.7.1 und Abb. 3.7.2 dargestellt in die Gleichungen (1) und (2) einsetzt, erhältst du die Komponenten der Kraftvektoren vorzeichenrichtig. Also positiv, wenn die Komponente in Achsenrichtung des Koordinatensystems wirkt und negativ, wenn sie entgegen der Achsenrichtung wirkt.
Warum? Schau die die Erläuterungen zu den Winkelfunktionen am Einheitskreis an. Dann wirst du verstehen, warum in 2D der Sinus im I. und II. Quadranten des Koordinatensystems (positive y-Achse) und der Kosinus im I. und IV. Quadranten (positive x-Achse) positiv sind.
Doch jetzt genug gedacht, zurück zur Aufgabenstellung:
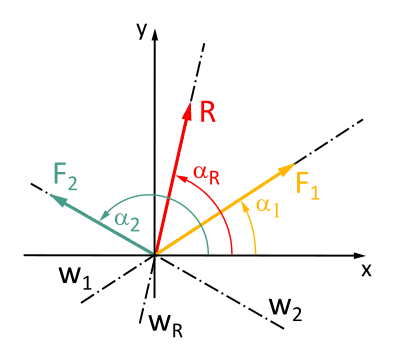
Sparen wir uns den Mathe-Kram, hier die Formeln:
(2.8)
Du möchtest es genauer wissen? Gerne, aber auf eigene Verantwortung!
So berechnest du F1: Nimm zunächst die Gleichungen (1) und (2) von oben. Multipliziere Gl. (1) mit \(\sin \alpha_2\) und Gl. (2) mit \(\cos \alpha_2\)
Jetzt ziehe die Gl. (4) von Gl. (3) ab:
und \(\sin 0 = 0\) bleibt schließlich:
So berechnest du F2: Nimm zunächst die Gleichungen (1) und (2) von oben. Multipliziere Gl. (1) mit \(\sin \alpha_1\) und Gl. (2) mit \(\cos \alpha_1\)
Jetzt ziehe die Gl. (9) von Gl. (8) ab:
und \(\sin 0 = 0\) bleibt schließlich:
Wegen \(\sin(-\varphi)=-\sin(\varphi)\) dürfen wir auch schreiben:
Es kommt eine Dimension hinzu, die z-Achse. Entsprechend hat die aufzuteilende Kraft R drei Komponenten: x, y und z. Damit ist es möglich, eine Kraft R im Raum in drei "Teilkräfte" F1, F2 und F3 aufzuteilen.
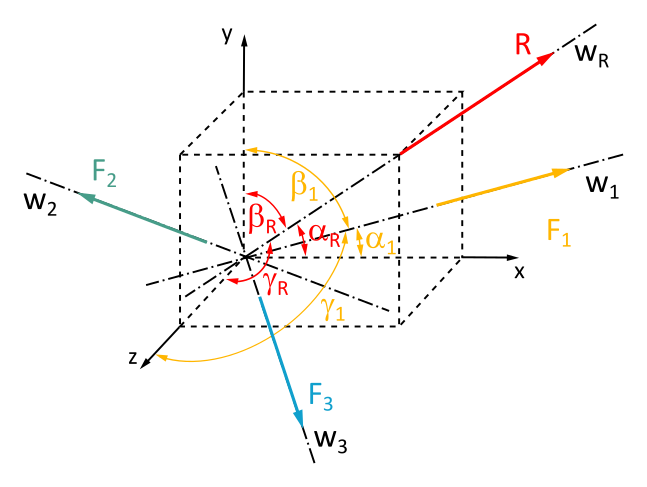
Der Richtungswinkel eines Vektors zur x-Achse sei \(\alpha\), der Richtungswinkel zur y-Achse \(\beta\) und der Richtungswinkel zur z-Achse \(\gamma\).
Kennst du die drei Richtungswinkel von R (\(\alpha_R\), \(\beta_R\) und \(\gamma_R\)) sowie die Richtungswinkel der Wirkungslinien w1 (\(\alpha_1\), \(\beta_1\) und \(\gamma_1\)), w2 (\(\alpha_2\), \(\beta_2\) und \(\gamma_2\)) und w3 (\(\alpha_3\), \(\beta_3\) und \(\gamma_3\)), dann erhälts du für jede Komponente eine Gleichung:
Dies ist ein Gleichungssystem aus drei Gleichungen für die drei Unbekannten F1, F2 und F3.
(2.9)
Lösbar ist die Gleichung (2.9) mit verschiedenen Verfahren, beispielsweise mit der Gaußschen Elimination oder der Cramer-Regel.
Das System besitzt eine eindeutige Lösung, wenn die drei Wirkungslinien der Vektoren nicht komplanar sind. Das bedeutet, dass die drei Vektoren nicht in derselben Ebene liegen, sondern einen dreidimensionalen Raum aufspannen.
Du kannst also jetzt eine Kraft in verschiedene "Teilkräfte" zerlegen, die in verschiedene Richtungen wirken.
Wie viele Richtungen du wählst, hängt davon ab, ob du dich in der Ebene oder im Raum befindest:
- Ebene: Hier kannst du die Kraft in genau zwei Richtungen zerlegen.
- Raum: Im 3D-Universum sind es genau drei Richtungen.
Das Coole: In beiden Fällen ist die Zerlegung eindeutig. Heißt: Es gibt nur eine richtige Lösung!
Aber Achtung: Mehr Richtungen, mehr Möglichkeiten! Willst du die Kraft in mehr als zwei oder drei Richtungen zerlegen, wird's kniffliger. Dann gibt es nämlich unendlich viele Möglichkeiten, das zu tun.
Ist das schlimm? Nicht unbedingt! Manchmal ist es sogar ganz praktisch, mehrere Zerlegungen zu haben. So kannst du zum Beispiel die Kraft auf verschiedene Teile einer Konstruktion verteilen.
Wichtig ist aber: Egal wie viele Richtungen du wählst, die Summe der Teilkräfte muss immer gleich der Hauptkraft sein. Und die Richtungen der Teilkräfte müssen so gewählt sein, dass sie zusammen die Richtung der Hauptkraft ergeben.
So einfach ist die Kraftzerlegung! Mit etwas Übung und den richtigen Tipps schaffst du das im Handumdrehen.
Eine Kraft F = 25 N soll in zwei rechtwinklig aufeinander stehende Komponenten F1 und F2 zerlegt werden. Die Wirklinien von F und F1 sollen den Winkel \(\alpha = 35°\) einschließen.
Ermittle grafisch und analytisch die Beträge von F1 und F2.
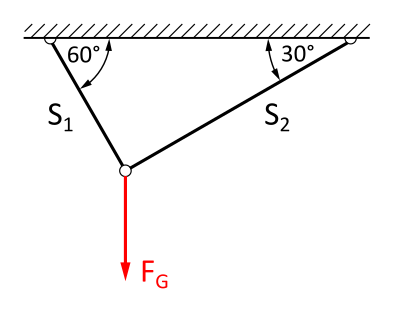
An zwei Seilen hängt eine Masse mit der Gewichtskraft FG.
Wie groß sind die Komponenten der Kraft FG = 10 kN in Richtung der Seile 1 und 2?
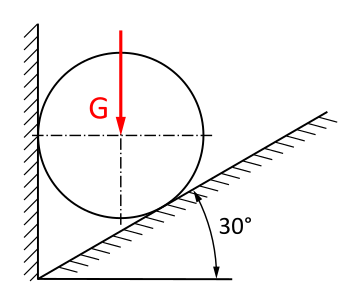
Eine Kugel liegt, wie dargestellt, in einer Vertiefung.
Wie groß sind die Komponenten der Gewichtskraft G = 40 kN in Richtung der Wände?
Hinweis:
Es können nur Kräfte normal (d.h. rechtwinklig) zur Wand übertragen werden.