Schritt 3: Querkraft \(Q_\eta\) als Funktion des Schnittwinkels \(\varphi\) bestimmen
Hey, Mathe-Checker! Hast du Bock auf eine kleine Schnitzeljagd? Wir jagen die Querkraft \(Q_\eta\) - aber die hat sich hinter dem gemeinen Schnittwinkel \(\varphi\) versteckt!
Keine Angst, ich bin dein treuer Sidekick! Gemeinsam knacken wir den Code und entlarven die geheime Formel.
-
Spickzettel zücken: Denk an unser geniales Kräftedreieck aus Abbildung 1.2.10. Da ist alles drin, was wir brauchen!
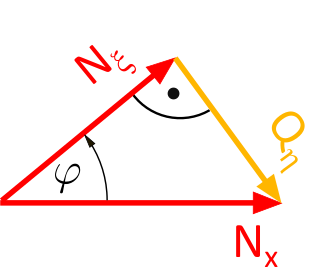
Abb. 1.2.10: Kräftedreieck aus Abbildung 1.2.5 - Geheimbotschaft entschlüsseln: Sieh dir die Gegenkathete \(Q_\eta\) und die Hypotenuse \(N_x\) genau an. Was fällt dir auf? Aha! Da ist ja ein trigonometrischer Zusammenhang versteckt!
-
Formel-Zauber: Mit etwas Sinus-Magie und der Gleichung
$$ \begin{align} \tag{1} \sin(\varphi) &= \dfrac{\mathrm{Gegenkathete}}{\mathrm{Hypotenuse}}\\[10pt] \tag{2} \sin(\varphi) &= \dfrac{Q_\eta}{N_x} \end{align} $$locken wir die Querkraft aus ihrem Versteck. Tadaaa!
-
Mission erfüllt! Jetzt hast du die Formel für \(Q_\eta\) in der Tasche:
$$ \begin{aligned} Q_\eta = N_x \cdot \sin(\varphi) \end{aligned} $$
(3)
Hui, war das nicht spannend? Mit dieser Formel kannst du die Querkraft berechnen, egal welchen Winkel der fiese \(\varphi\) auch zaubert.
Übrigens: Diese Formel ist zwar genial, aber nicht unfehlbar. Vergiss nicht, die Einheiten im Auge zu behalten!
P.S.: Wenn du noch mehr Mathe-Action brauchst, schau dir die trigonometrischen Beziehungen genauer an. Da gibt's noch mehr spannende Geheimnisse zu lüften!
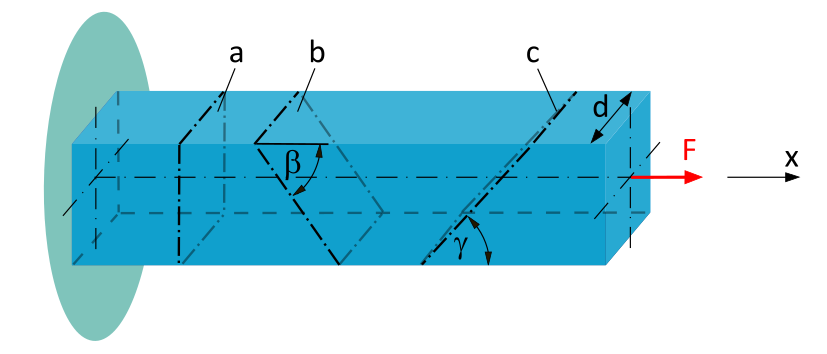
Normal- und Schubspannung unter beliebigem Schnittwinkel
Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge \(d=20~\mathrm{mm}\)) wird durch eine Zugkraft \(F=10~\mathrm{kN}\) in der Balkenachse belastet.
Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die
- in der Schnittebene a wirken.
- in der Schnittebene b (\(\beta = 50°\)) wirken.
- in der Schnittebene c (\(\gamma = 40°\)) wirken.