Schritt 4 | TechMechAcademy

Schritt 3: Querkraft

Q_{η}

als Funktion des Schnittwinkels

φ

bestimmen

Für welche Schnittwinkel

φ

sind die Normalspannung

σ_{ξ}

und die Schubspannung

τ_{ξ η}

maximal?

Auf dieser Seite

Übungsaufgaben

Inhaltsverzeichnis

Schritt 4: Aus den bisherigen Ergebnissen die Formeln für die Normalspannung $σ_{ξ}$ und die Schubspannung $τ_{ξ η}$ herleiten

Spannung pur - Knacke die Formelcodes!

Hey, Mathe-Genie! Bereit für die nächste Mission? Diesmal jagen wir die Formeln für die Normal- und Schubspannung bei einem beliebigen Schnittwinkel $φ$ .

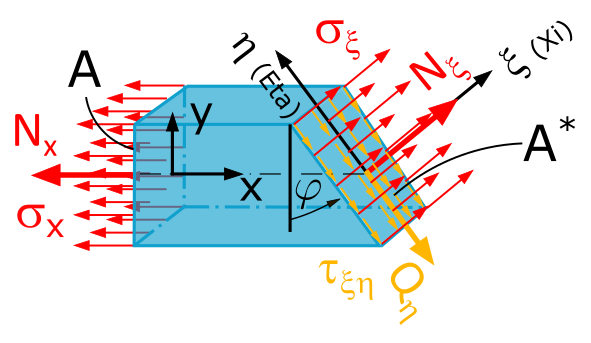
Diese Abbildung zeigt eine Schnittfläche unter einem beliebigen Schnittwinkel Phi und die in dieser Fläche wirkenden Normal- und Schubspannungen. — Abb. 1.2.11: Kräfte und Spannungen am gedrehten $x$ , $y$ -Koordinatensystem

Normalspannung

σ_{ξ}

Zuerst knacken wir den Code für $σ_{ξ}$ :

\begin{array}{r} (1) & σ_{ξ} = \frac{N_{ξ}}{A^{*}} \end{array}

Mit etwas Trigonometrie-Magie und unseren bisherigen Ergebnissen zaubern wir die Formel:

\begin{aligned} (2) & σ_{ξ} & = \frac{N_{x} \cdot \cos (φ)}{\frac{A}{\cos (φ)}} \\ (3) & σ_{ξ} & = \frac{N_{x} \cdot \cos (φ) \cdot \cos (φ)}{A} \\ (4) & σ_{ξ} & = \frac{N_{x}}{A} \cdot \cos^{2} (φ) \end{aligned}

Diese Gleichung können wir noch etwas vereinfachen. Da $σ_{x} = \frac{N_{x}}{A}$ gilt, erhalten wir

\begin{array}{r} (5) & σ_{ξ} = σ_{x} \cdot \cos^{2} (φ) \end{array}

Hui, ganz schön elegant, oder? $σ_{x}$ kennen wir ja schon und $φ$ ist einfach der Schnittwinkel. Aber Moment, da geht noch mehr! Mit einer weiteren trigonometrischen Formel können wir die Gleichung vereinfachen: Aus

\begin{array}{r} (6) & \cos^{2} (φ) = \frac{1}{2} (1 + \cos (2 φ)) \end{array}

folgt

\begin{array}{r} σ_{ξ} = \frac{σ_{x}}{2} (1 + \cos (2 φ)) \end{array}

(1.4)

Siehst du? Jetzt haben wir die Formel für $σ_{ξ}$ in ihrer ganzen Pracht!

Schubspannung

τ_{ξ η}

Weiter geht's mit der Schubspannung $τ_{ξ η}$ . Die Formel ist ähnlich, aber wir müssen aufpassen:

\begin{array}{r} (7) & τ_{ξ η} = \frac{Q_{η}}{A^{*}} \end{array}

Erneut zaubern wir mit etwas Trigonometrie-Magie und unseren bisherigen Ergebnissen die Formel:

\begin{aligned} (8) & τ_{ξ η} & = \frac{N_{x} \cdot \sin (φ)}{\frac{A}{\cos (φ)}} \\ (9) & τ_{ξ η} & = \frac{N_{x} \cdot \sin (φ) \cdot \cos (φ)}{A} \\ (10) & τ_{ξ η} & = \frac{N_{x}}{A} \cdot \sin (φ) \cdot \cos (φ) \end{aligned}

Diese Gleichung können wir noch etwas vereinfachen. Da $σ_{x} = \frac{N_{x}}{A}$ gilt, erhalten wir

\begin{array}{r} (11) & τ_{ξ η} = σ_{x} \cdot \sin (φ) \cdot \cos (φ) \end{array}

Mit einer weiteren trigonometrischen Formel können wir die Gleichung vereinfachen: Aus

\begin{array}{r} (12) & \sin (φ) \cdot \cos (φ) = \frac{1}{2} (\sin (2 φ)) \end{array}

folgt

\begin{array}{r} (13) & τ_{ξ η} = \frac{σ_{x}}{2} (\sin (2 φ)) \end{array}

Achtung! Diese Formel gilt nur für ein Koordinatensystem, in dem die Schubspannung nach unten rechts positiv ist.

Warum? Erinnern wir uns an dieser Stelle an das Vorzeichen der Schubspannung. Es hängt nämlich vom verwendeten Koordinatensystem ab.

Und wir sind von einer nach rechts unten positiven Schubspannung ausgegangen. Das kannst du im Kräftedreieck der Abbildung 1.2.10 nochmal überprüfen.

In anderen Koordinatensystemen müssen wir das Vorzeichen anpassen.

Formel-Wunder für gedrehte Koordinatensysteme:

$x$ , $y$ -System

$\begin{array}{r} τ_{ξ η} = - \frac{σ_{x}}{2} (\sin (2 φ)) \end{array}$

(1.5_xy)
$x$ , $z$ -System

$\begin{array}{r} τ_{ξ η} = \frac{σ_{x}}{2} (\sin (2 φ)) \end{array}$

(1.5_xz)

Geschafft! Mit diesen Formeln kannst du die Normal- und Schubspannung bei jedem Schnittwinkel berechnen.

Übrigens: Diese Formeln sind zwar genial, aber nicht unfehlbar. Vergiss nicht, die Einheiten im Auge zu behalten!

P.S.: Lust auf mehr Mathe-Action? Dann schau dir die trigonometrischen Beziehungen genauer an. Da gibt's noch mehr spannende Geheimnisse zu lüften!

Extra Tipp: Diese Formeln sind super praktisch, wenn du Spannungen in Bauteilen berechnen musst. So kannst du zum Beispiel herausfinden, ob ein Bauteil einer bestimmten Belastung standhält. ️

Übungsaufgabe

Aufgabe F-1.1.4

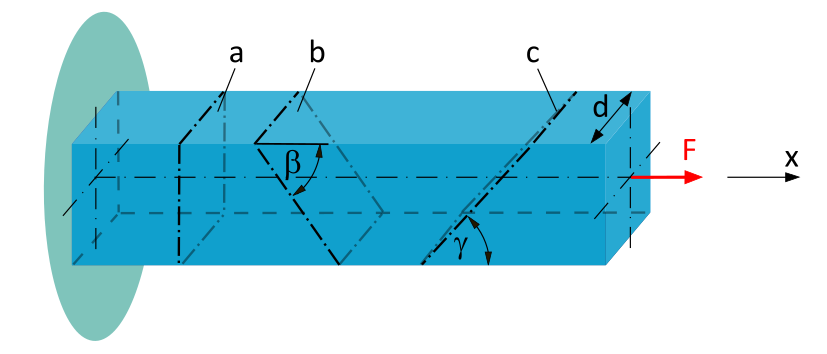
Die Abbildung zeigt einen linksseitig eingespannten Balken mit quadratischem Querschnitt. In der Zeichung sind drei Schnittebenen a, b und c angedeutet. Die Schnittebene a ist senkrecht zur Balkenachse. Die Schnittebene b verläuft von links oben nach rechts unten, der gegebene Winkel Beta beschreibt den kleineren Winkel oben. Die Schnittebene c verläuft von links unten nach rechts oben, der gegebene Winkel Gamma beschreibt den kleineren Winkel unten. Die Seitenlänge des Querschnittes ist die Länge d. Am rechten Balkenende wirkt eine Zugkraft F im Schwerpunkt des Querschnitts.

Normal- und Schubspannung unter beliebigem Schnittwinkel

Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge $d = 20 mm$ ) wird durch eine Zugkraft $F = 10 kN$ in der Balkenachse belastet.

Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die

in der Schnittebene a wirken.
in der Schnittebene b ( $β = 50 °$ ) wirken.
in der Schnittebene c ( $γ = 40 °$ ) wirken.

Festigkeitslehre / Elastostatik

Spannungszustand: Tauche ein in die Welt der Kräfte und Spannungen!

Schritt 4: Aus den bisherigen Ergebnissen die Formeln für die Normalspannung $σ_{ξ}$ und die Schubspannung $τ_{ξ η}$ herleiten

Normal- und Schubspannung unter beliebigem Schnittwinkel

Festigkeitslehre / Elastostatik

Spannungszustand: Tauche ein in die Welt der Kräfte und Spannungen!

Schritt 4: Aus den bisherigen Ergebnissen die Formeln für die Normalspannung σξ und die Schubspannung τξη herleiten

Normal- und Schubspannung unter beliebigem Schnittwinkel

Schritt 4: Aus den bisherigen Ergebnissen die Formeln für die Normalspannung $σ_{ξ}$ und die Schubspannung $τ_{ξ η}$ herleiten