Übungsaufgabe F-6.1.4 TechMech 2 Festigkeitslehre

Aufgabe F-6.1.4

Flächenträgheitsmoment: Axiales und Biaxiales Flächenträgheitsmoment bestimmen

Aufgabenstellung

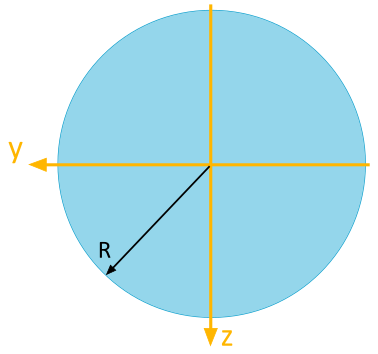
Kreisfläche, für die das Flächenträgheitsmoment (axial, biaxial) berechnet werden soll. Radius: R, Zentrum: y,z, y nach links positiv, z nach unten positiv. — Abb. 1: Kreisfläche mit Schwerachsen

Für die abgebildete Kreisfläche sind folgende Flächenträgheitsmomente bezüglich des dargestellten $y$, $z$-Koordinatensystems zu bestimmen:

Axiales Flächenträgheitsmoment $I_y$
Axiales Flächenträgheitsmoment $I_z$
Biaxiales Flächenträgheitsmoment $I_{yz}$

Kurzlösung

a) Bestimme das axiale Flächenträgheitsmoment $I_y$

$$ \begin{aligned} I_y&= \dfrac{1}{4}R^4\pi \end{aligned} $$

b) Bestimme das axiale Flächenträgheitsmoment $I_z$

$$ \begin{aligned} I_z &= \dfrac{1}{4}R^4\pi \end{aligned} $$

c) Bestimme das biaxiale Flächenträgheitsmoment $I_{yz}$

$$ \begin{aligned} I_{yz} &= 0 \end{aligned} $$

Ausführlicher Lösungsweg

Ein Ansatz zur Bestimmung der Flächenträgheitsmomente besteht darin, die Berechnung in Polarkoordinaten durchzuführen.

Um die Berechnungsmethode anwenden zu können, ist es erforderlich, den funktionalen Zusammenhang $r(\varphi)$ zu ermitteln.

Diesen finden wir, wenn wir uns für den Kreis den Zusammenhang von einem beliebigen Winkel $\varphi$ und dem dazugehörigen Radius $r(\varphi)$ des Kreises verdeutlichen: Der Radius ist konstant. Diese Eigenschaft des Kreises vereinfacht die Berechnung nach dieser Methode. Sie ist daher bei der Berechnung kreisförmiger Flächen den Berechnungsmethoden mit kartesischen Koordinaten zu bevorzugen.

Weiterlesen mit TechMechAcademy+

Alles. Immer. Überall.

Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.

Werde ein TechMechAcademy+ Premiummitglied!

Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.